Pandemia por Covid-19 14 Jul 2020 9:20 AM (4 years ago)
 Olá a todos!
Olá a todos!
Deixo-vos aqui alguns vídeos sobre os cuidados que devemos ter neste tempo de Pandemia...
Escola.org 6 Aug 2018 4:56 AM (6 years ago)
Olá a todos!
Aqui vos deixo um site com exercícios interativos.
O site está organizado de forma simples.
Podem encontrar os temas que vos interessa clicando em Ctrl+F. Abre depois um espacinho com uma lupa e só têm de escrever sobre o que querem encontrar.
Bons exercícios!
https://www.escola.org/exercicios/?ity_ef_rule=list
Lista de links para questionários online Ciências Naturais (Kahoot) 19 Jul 2018 5:30 AM (6 years ago)
(podes instalar a app Kahoot no teu telemóvel e divertires-te a fazer os questionários)
PROCESSOS VITAIS COMUNS AOS SERES VIVOS
Trocas nutricionais entre o
organismo e o meio: nos animais
Trocas nutricionais entre o
organismo e o meio: nas plantas
Transmissão de vida: reprodução
no ser humano
- Quiz,
- Quiz1
Transmissão de vida: nas
plantas
AGRESSÕES DO MEIO E INTEGRIDADE DO ORGANISMO
Microrganismos
- Quiz
Higiene e problemas sociais
Lista de links para questionários online Matemática (Kahoot) 19 Jul 2018 5:28 AM (6 years ago)
(podes instalar a app Kahoot no teu telemóvel e divertires-te a fazer os questionários)
Números e Operações
Números racionais não negativos
- Frações irredutíveis;
- Redução de duas frações ao mesmo denominador;
- Ordenação de números racionais representados por frações;
- Adição, subtração, multiplicação e divisão de números racionais não negativos representados na forma de fração;
- Representação de números racionais na forma de numerais mistos; adição e subtração de números racionais representados por numerais mistos;
- Aproximações e arredondamentos de números racionais;
- Problemas de vários passos envolvendo números racionais representados na forma de frações, dízimas, percentagens e numerais mistos.
Números naturais
- Determinação do máximo divisor comum de dois números naturais por inspeção dos divisores de cada um deles;
- Algoritmo de Euclides;
- Números primos entre si; números obtidos por divisão de dois dados números pelo respetivo máximo divisor comum; irredutibilidade das frações de termos primos entre si;
- Determinação do mínimo múltiplo comum de dois números naturais por inspeção dos múltiplos de cada um deles;
- Relação entre o máximo divisor comum e o mínimo múltiplo comum de dois números;
- Problemas envolvendo o cálculo do mínimo múltiplo comum e do máximo divisor comum de dois números.
Geometria e Medida
Ângulos, paralelismo e perpendicularidade - Ângulo igual à soma de outros dois; definição e construção com régua e compasso;- Bissetriz de um ângulo; construção com régua e compasso;
- Ângulos complementares e suplementares;
- Igualdade de ângulos verticalmente opostos;
- Semirretas diretamente e inversamente paralelas;
- Ângulos correspondentes e paralelismo;
- Ângulos internos, externos e pares de ângulos alternos internos e alternos externos determinados por uma secante num par de retas concorrentes; relação com o paralelismo;
- Ângulos de lados diretamente e inversamente paralelos; pares de ângulos de lados perpendiculares.
Triângulos e quadriláteros
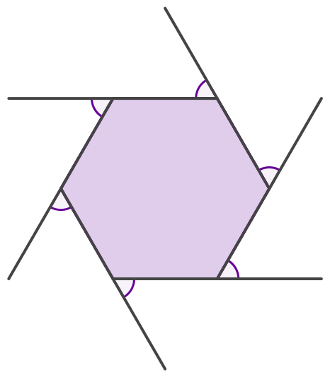
- Ângulos internos, externos e adjacentes a um lado de um polígono;- Ângulos de um triângulo: soma dos ângulos internos, relação de um ângulo externo com os internos não adjacentes e soma de três ângulos externos com vértices distintos;
- Triângulos acutângulos, obtusângulos e retângulos; hipotenusa e catetos de um triângulo retângulo;
- Ângulos internos de triângulos obtusângulos e retângulos;
Link
- Paralelogramos; ângulos opostos e adjacentes de um paralelogramo;
- Critérios de igualdade de triângulos: critérios LLL, LAL e ALA; construção de triângulos dados os comprimentos de lados e/ou as amplitudes de ângulos internos;
- Relações entre lados e ângulos num triângulo ou em triângulos iguais;
- Igualdade dos lados opostos de um paralelogramo;
- Desigualdade triangular;
- Pé da perpendicular traçada de um ponto para uma reta e, num dado plano, perpendicular a uma reta num ponto;
- Distância de um ponto a uma reta e entre retas paralelas; altura de um triângulo e de um paralelogramo.
Problemas
- Problemas envolvendo as noções de paralelismo, perpendicularidade, ângulos e triângulos.Área
- Área de retângulos de lados de medida racional;- Fórmulas para a área de paralelogramos e triângulos;
Link
- Problemas envolvendo o cálculo de áreas de figuras planas.
Amplitude de ângulos
- Medidas de amplitudes de ângulos;
- O grau como unidade de medida de amplitude; minutos e segundos de grau;
- Utilização do transferidor para medir amplitudes de ângulos e para construir ângulos de uma dada medida de amplitude;
- Problemas envolvendo adições, subtrações e conversões de medidas de amplitude expressas em forma complexa e incomplexa.
Álgebra
Expressões algébricas e propriedades das operações- Prioridades convencionadas das operações de adição, subtração, multiplicação e divisão; utilização de parêntesis;
- Propriedades associativa e comutativa da adição e multiplicação e propriedades distributivas da multiplicação em relação à adição e subtração;
- Elementos neutros da adição e da multiplicação e elemento absorvente da multiplicação de números racionais não negativos;
- Utilização do traço de fração com o significado de quociente de números racionais;
- Inversos dos números racionais positivos;
- Produto e quociente de quocientes de números racionais; inverso de um produto e de um quociente de números racionais;
- Cálculo de expressões numéricas envolvendo as quatro operações aritméticas e a utilização de parêntesis;
- Linguagem natural e linguagem simbólica.
Revisão números racionais
Organização e Tratamento de Dados
Gráficos cartesianos
- Referenciais cartesianos, ortogonais e monométricos;- Abcissas, ordenadas e coordenadas;
- Gráficos cartesianos.
Representação e tratamento de dados
- Tabelas de frequências absolutas e relativas;- Gráficos de barras e de linhas;
- Média aritmética;
- Problemas envolvendo a média e a moda;
- Problemas envolvendo dados em tabelas, diagramas e gráficos.
link
Link 1
Revisões 5º ano matemática
6º ano
Números e Operações
Números naturais
- Números primos;
- Crivo de Eratóstenes;
- Teorema fundamental da aritmética e aplicações.
Números racionais positivos e negativos
Link
- Números racionais negativos;
- Simétrico e valor absoluto de um número racional;
- Semirreta de sentido positivo associada a um número; ordenação de números racionais;
- Conjunto dos números inteiros relativos e conjunto dos números racionais.
Adição e subtração de números racionais
- Segmentos de reta orientados; orientação positiva e negativa de segmentos orientados da reta numérica;
- Adição de números racionais; definição e propriedades;
- Subtração e soma algébrica de números racionais; definição e propriedades;
- Módulo da diferença de dois números como medida da distância entre os pontos que representam esses números na reta numérica.
Link
Decimais frações e percentagem relações
Revisões números racionais
Geometria e Medida
Figuras geométricas planas
Link
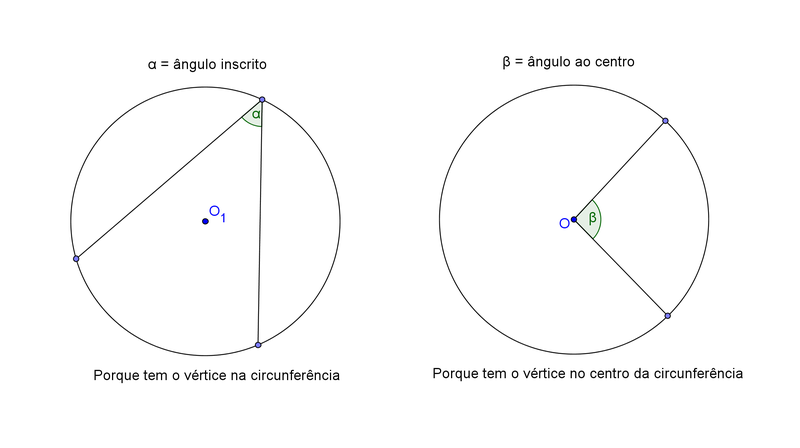
- Ângulo ao centro e setor circular;
- Polígonos inscritos numa circunferência;
- Retas e segmentos de reta tangentes a uma circunferência;
- Polígonos circunscritos a uma circunferência;
- Apótema de um polígono.
Sólidos geométricos e propriedades
Link
- Prismas; prismas oblíquos e regulares;
- Pirâmides;
- Bases, faces laterais e vértices de prismas e pirâmides;
- Pirâmides regulares;
- Cilindros; bases, eixo, geratrizes e superfície lateral de um cilindro;
- Cones; base, vértice, eixo, geratrizes e superfície lateral de um cone;
- Cilindros e cones retos;
- Relação entre o número de arestas e de vértices de um prisma (ou pirâmide) e da respetiva base;
- Poliedros convexos;
- Relação de Euler;
- Planificações de sólidos;
- Problemas envolvendo sólidos geométricos e respetivas planificações.
Revisões sólidos
Área
Perímetro e área de polígonos
- Fórmula para o perímetro do círculo; aproximação por perímetros de polígonos regulares inscritos e circunscritos;
- Fórmula para a área de polígonos regulares;
- Fórmula para a área do círculo; aproximação por áreas de polígonos regulares inscritos;
- Problemas envolvendo o cálculo de perímetros e áreas de polígonos e círculos.
Sólidos e áreas
Círculo e cirfunferência
Perímetros e áreas
Volume
- Fórmula para o volume do paralelepípedo retângulo com dimensões de medida racional;
- Fórmulas para o volume do prisma reto e do cilindro reto;
- Problemas envolvendo o cálculo de volumes de sólidos.
Áreas e volume 6º ano
Isometrias do plano
- Reflexão central como isometria; invariância da amplitude de ângulo;
- Mediatriz de um segmento de reta; construção da mediatriz utilizando régua e compasso;
- Reflexão axial como isometria; invariância da amplitude de ângulo; eixos de simetria; a bissetriz de um ângulo como eixo de simetria;
- Rotação de sentido positivo ou negativo como isometria; invariância da amplitude de ângulo;
- Imagem de um segmento de reta por uma isometria;
- Construção de imagens de figuras planas por reflexões centrais e axiais e por rotações;
- Simetrias de rotação e de reflexão; Simetria conceito
- Problemas envolvendo as propriedades das isometrias e utilizando raciocínio dedutivo;
- Problemas envolvendo figuras com simetrias de rotação e de reflexão axial.
Link revisões
Link revisões 1
Link
Link ótimo
Álgebra
Potências de expoente natural
link
- Potência de base racional não negativa;
- Regras operatórias das potências de base racional não negativa;
- Prioridade das operações;
- Linguagem simbólica e linguagem natural em enunciados envolvendo potências.
Sequências e regularidades
- Determinação de termos de uma sequência definida por uma lei de formação recorrente ou por uma expressão geradora;
- Determinação de expressões geradoras de sequências definidas por uma lei de formação recorrente;
- Problemas envolvendo a determinação de uma lei de formação compatível com uma sequência parcialmente conhecida.
Proporcionalidade direta
- Noção de grandezas diretamente proporcionais e de constante de proporcionalidade direta;
- Proporções; extremos, meios e termos de uma proporção; propriedades; regra de três simples;
- Escalas em mapas;
- Problemas envolvendo a noção de proporcionalidade direta entre grandezas mutuamente dependentes.
Link
Organização e Tratamento de Dados
Representação e tratamento de dados
Link
Link 1
- População e unidade estatística;
- Variáveis quantitativas e qualitativas;
- Gráficos circulares;
- Análise de conjuntos de dados a partir da média, moda e amplitude;
- Problemas envolvendo dados representados de diferentes formas.
SuperTmatik 17 Mar 2017 2:30 PM (8 years ago)
Gostas de jogar o jogo do SuperTmatik?
Queres jogar online?
Podes ir ao site Eudactica.pt e clicar no link: http://www.supertmatik.net/app/cartas/ Neste caso é
Junta-te a um colega/amigo, pega numa caneta e num papel e diverte-te.
Descobre Portugal em números 27 Aug 2016 5:14 AM (8 years ago)
 Olá a todos,
Olá a todos,
soube da existência de um site onde podes encontrar imensa informação sobre o nosso país, relativamente a:
- Ambiente
- Ciência e tecnologia
- Cultura e desporto
- Educação
- Emprego
- Família
- Justiça
- População
- Saúde
- Turismo
Vê o vídeo de apresentação:
Tens aqui a página web da Pordata kids ("Por" de Portugal, "data" de números e "kids" do inglês que quer dizer criança). Basta clicar nela para abrir.
Podes descarregar jogos no site em : http://www.pordatakids.pt/Jogos
Erro nos links... 29 Jul 2016 9:25 AM (8 years ago)
 Olá caros alunos,
Olá caros alunos,
venho pedir-vos que se encontrarem algum problema em abrir um link de um jogo, ou de uma ficha me informem, por exemplo, fazendo um comentário.
Para facilitar a entrada nos diferentes links, arranja um programa que bloqueie os Pop-ups.

Bom trabalho!!
Contactar o autor do blog. 29 Jul 2016 3:30 AM (8 years ago)
Olá a todos.
Caso estejam interessados em colocar-me alguma questão, façam-no mais abaixo ou aqui.
Não se esqueçam de deixar o email.
Só respondo a mensagens que têm haver com as disciplinas de matemática ou ciências naturais de 1º e 2º ciclo! Podem ver a resposta aqui.
A carregar...
Grupo para colocar questões e opiniões 28 Jul 2016 11:18 AM (8 years ago)
 Olá!
Olá!
Hoje aprendi a criar um grupo com a possibilidade de criar um fórum.
Assim podemos discutir alguma temática aqui apresentada, ou podem colocar dúvidas sobre algum conteúdo. Para isso basta ter uma conta no google, como por exemplo ter um email do Gmail!
Cliquem em http://groups.google.com/group/ajudaalunos
Página no Facebook 27 Jul 2016 12:30 PM (8 years ago)
 Pode utilizar a página do Facebook:
Pode utilizar a página do Facebook:
https://www.facebook.com/groups/132117906817594/
AJUDAALUNOS com material, novidades, atividades, tarefas, etc, sobre matemática e ciências naturais.
Propriedades do ar e dos gases 19 Jan 2015 10:53 AM (10 years ago)

Aqui vos deixo algumas experiências para demonstrar as propriedades do ar e seus componentes.
Propriedades do ar- Ar tem peso
Propriedades do ar - Ar pode ser comprimido
Propriedade do ar - Ar ocupa espaço
Propriedade do oxigénio- Comburente
Propriedade do nitrogénio ou azoto - Incomburente
Propriedade do dióxido de carbono - Incomburente
(Vejam a conclusão mais abaixo)
"O que apagou a vela? A garrafa apenas se aproximou da chama e ela já se apagou. O que ocorreu? Ao colocar Bicarbonato de Sódio na garrafa com vinagre, ocorreu uma reação química que libertou dióxido de carbono. Esse gás se acumulou na garrafa e, quando ela foi tombada em direção à chama, escorreu em direção à vela tomando o lugar do Gás Oxigénio (Comburente essencial para que ocorra a combustão). Assim, a chama se apagou por falta de Oxigénio.
Carlos Eduardo Godoy
Professor de Ciências da Natureza e Tecnologia
www.cecgodoy.pro.br"
Educação ambiental para a sustentabilidade 28 Nov 2014 1:40 PM (10 years ago)
Deixo-vos com uma apresentação em powerpoint sobre este tema.
É importante que percebam a situação do nosso planeta e saibam o que podemos fazer para evitar todos os problemas.
Simulacro de um sismo 8 Oct 2014 10:52 AM (10 years ago)
Olá a todos,
convido-os a convidar os vossos professores, colegas e amigos a fazer um simulacro de um sismo na próxima segunda feira.
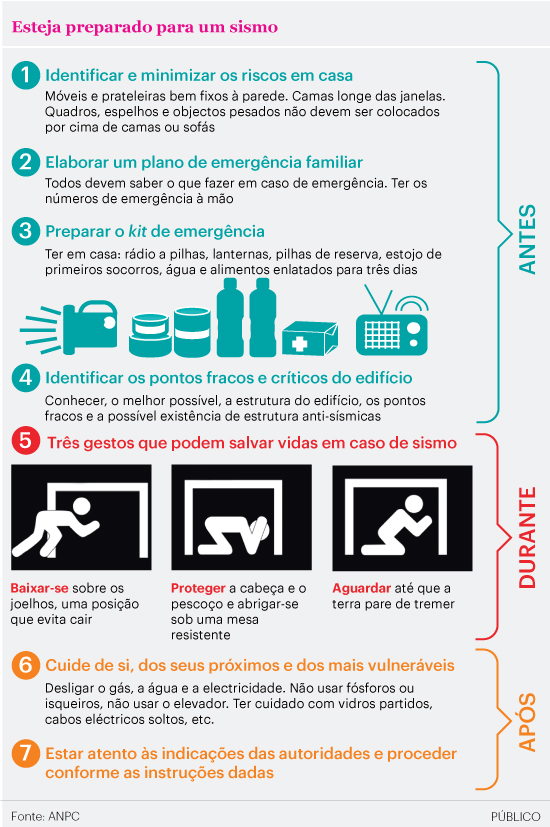
A terra vai tremer em Portugal exactamente às 10h13 da próxima segunda-feira, dia 13. E eis o que todos têm a fazer: baixar-se, para evitar uma queda, abrigar-se sob uma mesa e esperar um minuto até que o sismo passe.
Calma, é apenas um exercício nacional de preparação dos cidadãos para o risco sísmico. A Autoridade Nacional de Protecção Civil (ANPC) está a convidar toda a população a participar – onde quer que as pessoas estejam, nas escolas, empresas, em centros comerciais ou em casa. Se os portugueses aderirem em força, muitas mortes ou ferimentos podem ser evitados num terramoto real no país.
Num sismo, o desespero pode fazer com que qualquer um corra para a rua, com medo de que a casa lhe caia em cima. Mas o mais seguro, segundo a ANPC, é proteger-se logo que o tremor é sentido.
A primeira atitude é baixar-se, para evitar que o corpo seja derrubado ou arremessado contra o chão. Depois, deve-se procurar refúgio debaixo de uma mesa sólida e lá permanecer até que o sismo passe. “Se estivermos dentro de casa, é esta a atitude mais segura”, garante Anabela Saúde, responsável pela área da comunicação na ANPC. “Há um consenso sobre o facto de grande parte dos danos corporais num sismo ter a ver com a queda de objectos sobre as pessoas”, completa."
Segurança 9 Jul 2014 12:17 PM (10 years ago)
Olá a todos!
Como ando a fazer uma formação sobre a Proteção Civil e sobre os cuidados a ter quando acontece um sismo, um incêndio ou outro incidente deixo-vos:
- uns panfetos sobre situações que nos podem acontecer e formas de diminuir os riscos de ficarmos feridos. (basta clicares em cada palavra sublinhada e uma janela abrir-se-á.
O que fazer quando há um Incêndio na escola???
E quando há um Sismo ou tremor de terra?
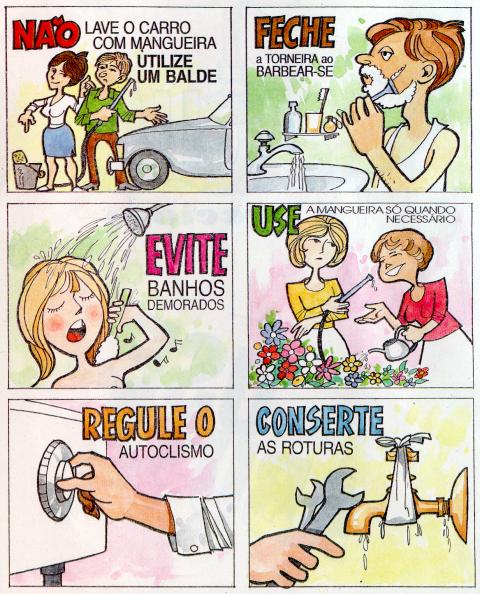
Quando há falta de água deves...
Deparas-te com uma situação de inundação como deves reagir?
Nesta época do ano estamos na altura dos incêndios florestais. Como agir nestes casos?
Agir durante um incêndio em casa...
Agora que estás de férias deves ter em conta algumas regras se fores para a montanha ou para o campo.
Podes ouvir alguns conselhos sobre incêndios, água, calor e cheias/inundações, aqui.
- alguns vídeos que deves ver com atenção e mostrar aos teus amigos e familiares, sobre os cuidados a ter com a tua segurança e dos outros.
No próximo filme podes aprender como deves proceder quando há um incêndio ou sismo na tua escola.
Pode salvar-te!
Já ouviste falar no Tinoni e companhia, deixo-te um filme sobre isso: (para veres outros clica onde diz, Lista de Reprodução e escolhe outro filme) Diverte-te e aprende. Assim estás a proteger-te!
Blog sobre animais 14 Apr 2014 10:10 AM (10 years ago)
 Olá caros alunos,
Olá caros alunos,
aqui vos deixo um blog que estou a criar, em conjunto com alunos meus, sobre BI dos animais.
O objetivo é criar B.I. de animais diferentes para tornar esta página mais rica!
Se estiveres interessado em participar neste projeto envia, via email, o documento que queres ver publicado!
Boas pesquisas!
Dia do Pi 14 Mar 2014 12:41 PM (11 years ago)
 Hoje comemora-se o dia do Pi.
Hoje comemora-se o dia do Pi.
Os alunos a partir do 2º ciclo ficam a conhecer o pi e aqui vos deixo algumas informações sobre ele.
O Dia do Pi é comemorado anualmente no dia 14 de Março. A escolha da data 3 de Março para o Dia do Pi prende-se com o facto da notação americana das datas ser mês/dia e não dia/mês.
Assim, nos Estados Unidos da América, a notação do dia 14 de Março é 3/14, a aproximação mais conhecida de Pi (3,141592653589793238462643383...)
O auge das comemorações acontece à 1:59 da tarde (porque 3,14159 = π arredondado até a 5ª casa decimal).
Origem do Dia do Pi
O que é o Pi?
O número pi (representado habitualmente pela letra grega
Se pensarmos que ao dar a volta à Lua seguindo um dos seus círculos máximos, percorremos aproximadamente 10920 Km e se dividirmos este valor pelo diâmetro da Lua que é 3476 Km iremos verificar que esta razão é de 3,14154200…, este número é-nos familiar, é aproximadamente 3,14.
No dia 14 de Março é também celebrado o aniversário de nascimento de Albert Einstein (nascido a 14 de março de 1879)
Em 14 de março de 2004, Daniel Tammet recitou pi até o 22514ª dígito, obtendo o recorde europeu pelo feito.
Sobre o pi...
Mais informações sobre o pi...
http://www.educ.fc.ul.pt/icm/icm98/icm11/
Sustentabilidade ambiental 3 Jan 2014 12:45 PM (11 years ago)
 Hoje vamos aprender o que quer dizer o conceito de Sustentabilidade ambiental.
Hoje vamos aprender o que quer dizer o conceito de Sustentabilidade ambiental.
Nunca antes se ouviu falar tanto nessa palavra quanto nos dias atuais: Sustentabilidade. Mas, afinal de contas, o que é sustentabilidade?
“Na prática” sustentabilidade representa promover a exploração de áreas ou o uso de recursos planetários (naturais ou não), de forma a prejudicar o menos possível o equilíbrio entre o meio ambiente e as comunidades humanas e toda a biosfera que dele dependem para existir.
Assim, os projetos empresariais que tenham por base a sustentabilidade, começaram a multiplicar-se e a espalhar-se por vários lugares antes degradados do planeta. Muitas comunidades que antes viviam sofrendo com doenças de todo tipo; provocadas por indústrias poluidoras instaladas na sua vizinhança viram a sua qualidade de vida ser recuperada, aos poucos e melhorada ao longo do desenvolvimento desses projetos sustentáveis.
A exploração e a extração de recursos com mais eficiência e com a garantia da possibilidade de recuperação das áreas degradadas é a chave para que a sustentabilidade seja uma prática bem sucedida e aplicada com muito mais frequência aos grandes empreendimentos.
De uma forma simples, podemos afirmar que garantir a sustentabilidade de um projeto ou de uma região determinada; é dar garantias de que mesmo explorada essa área continuará a dar recursos e bem estar natural, econômico e social para as comunidades que nela vivem por muitas e muitas gerações. Mantendo a força vital e a capacidade de regenerar-se mesmo diante da ação contínua e da presença da mão humana.
A Sustentabilidade Ambiental é a capacidade de manter o ambiente natural viável à manutenção das condições de vida para as pessoas e para as outras espécies.
Isso garante, ainda, a qualidade de vida para o homem, tendo em conta a habitabilidade, a beleza do ambiente e a sua função como fonte de energias renováveis.
A adoção das medidas que dêem sustentação ambiental garante, em médio e longo prazo, um planeta em boas condições para o desenvolvimento das diversas formas de vida, inclusive a humana, garantindo a manutenção dos recursos naturais (florestas, matas, rios, lagos, oceanos) necessários para a qualidade de vida das próximas gerações.
Exemplos de ações sustentáveis e ambientais:
- procura de substitutos ecologicamente aceitável, como as energias renováveis, ao petróleo, que além de altamente poluente, tende a esgotar-se ainda mais rápido por conta do aumento do consumo ao longo dos séculos XX e XXI;

- Exploração dos recursos minerais (petróleo, carvão, minérios) de forma controlada, racionalizada e com planeamento;
- utilização da agricultura orgânica/biológica, termo usado para designar a produção de alimentos e outros produtos vegetais que não faz uso de produtos químicos sintéticos ou organismos geneticamente modificados, que agridem a natureza e são prejudiciais à saúde. A agricultura orgânica ganha caráter sustentável, pois persegue três objetivos principais: a conservação do meio ambiente, a formação de unidades agrícolas lucrativas e a criação de comunidades agrícolas prósperas;
- exploração dos recursos vegetais de florestas e matas, garantindo o replantação das plantas;
- preservação de áreas verdes não exploradas economicamente;
- uso de fontes de energia limpas e renováveis (eólica, geotérmica e hidráulica);
- reciclagem dos resíduos sólidos e exploração do gás libertado em aterros sanitários como fonte de energia;
- Desenvolvimento da gestão sustentável nas empresas para diminuir o desperdício de matéria-prima e desenvolvimento de produtos com baixo consumo de energia.
Múltiplos e divisores 15 Nov 2013 2:18 PM (11 years ago)

O múltiplo de um número é um número se pode obter multiplicando o primeiro por qualquer número natural. Por exemplo, os múltiplos de 2 são todos os números pares, que terminam em 0, 2, 4, 6 e 8.
Em linguagem mais simples os múltiplos de um número designam-se pelos números da tabuada desse número.
Escreve-se:
M2={0, 2, 4, 6, 8, 10, 12, 14, 16, 18, ...}
M3={0, 3, 6, 9, 12, 15, 18, 21, 24, 27, ...}
M10={0,10, 20, 30, 40, 50, 60, ...}
Podemos concluir que:
- o zero é múltiplo de qualquer número;
- o conjunto de múltiplos de um qualquer número é infinito.
O divisor de um número é um número que pode dividir o primeiro. Quando se refere a "poder dividir" quer dizer que na divisão inteira o resto é sempre zero.
Em linguagem corrente pode afirmar-se que os dividores de um número são as tabuadas onde aquele primeiro número se encontra.
Por exemplo os divisores de 4, são o 1, 2 e 4. Os divisores de 21 são, 1, 3, 7 e 21.
Escreve-se:
D4={1, 2, 4}
D21={1, 3, 7, 21}
D100={1, 2, 4, 5, 10, 20, 25, 50, 100}
Podemos concluir que:
- um é divisor de qualquer número;
- o conjunto dos divisores de qualquer número é finito.
Podemos observar algumas propriedades dos divisores
1ª propriedade
Num produto de fatores, um divisor comum dos fatores é também divisor do resultado (produto).
12 x 4 = 28
(3 x 2 x 2) x (2 x 2)
28 é então divisível por 4 e 2, ou seja, os divisores comuns do 12 e do 4.
4 x 10 = 40
(2 x 2) x (2 x 5)
40 é divisível por 2, 4 ou seja os divisores comuns de 4 e de 10.
2ª propriedade
Se um número natural é divisor de dois outros números, então também é divisor da soma e da diferença desses dois números.
12 + 4 = 16
(2 x 6) +(2 x 2)
O divisor comum entre o 4 e o 12 é o número 2, logo o 2 também é divisor de 16.
21 - 6 = 15
(3 x 7) - (3 x 2)
O divisor comum entre 21 e 6 é o número 3, logo 3 também é divisor de 15.
3ª propriedade
Numa divisão inteira, os divisores comuns do dividendo e do divisor também são divisores do resto.
4ª propriedade
Numa divisão inteira, os divisores comuns ao divisor e ao resto também são do dividendo.
Faz os seguintes exercícios:
- http://www.atividadesdematematica.com/atividade-de-matematica-para-o-7-ano/multiplos-e-divisores
- http://www.clq1.com.br/clq/noticias/files/314/Multiplos_e_divisores6.pdf
- http://quintalestudante.blogspot.pt/2013/07/atividades-com-multiplos-divisores-e.html
Curiosidades na ciência! 7 Nov 2013 12:33 PM (11 years ago)
como sou muito curiosa deixo-vos algumas curiosidades interessantes sobre as ciências... Cada uma delas foi obtida a partir de pesquisas feitas na internet!
Curiosidades do planeta Terra
Por que perdemos os dentes de leite?
Desde o nascimento, as raízes dos dentes de leite e dos dentes definitivos estão dentro das gengivas. Os dentes de leite nascem entre os 6 meses e os 2 anos de idade. Perto dos 6 anos, as raízes dos dentes definitivos desenvolvem-se e os dentes de leite caem para dar lugar a eles.
Até que idade crescemos?
O crescimento dos ossos começa com o nascimento e vai até, mais ou menos, até aos 20 anos. Porém, o esqueleto não é o único a modificar-se. Na adolescência, todo o corpo muda: é a puberdade. Quando ficamos adultos, o corpo não cresce mais.
Por que é que os nossos dentes não têm a mesma forma?
Os dentes da frente, incisivos servem para cortar os alimentos. Eles são chatos e cortantes. Os caninos rasgam os alimentos. Eles são muito pontiagudos. Os molares são grandes e largos, servem para triturar a comida.
Para que serve a saliva?
A saliva é importante para matar os micróbios e deixar a boca húmida. Quando comemos, a saliva molha os alimentos e assim começa a digestão. Isso facilita muito o trabalho de todo o sistema digestivo!
Porque ficamos bronzeados quando apanhamos sol?
A pele é muito sensível a certos raios do sol, os ultravioletas. Para se proteger, ela fabrica uma substância escura, a melanina. Quando ficamos expostos ao sol, essa substância é fabricada em maior quantidade e ficamos bronzeados. Mas não podemos esquecer-nos do protetor solar.
Por que é que as pessoas morrem?
Na velhice, os órgãos já não funcionam tão bem. O corpo cansa-se e tem mais dificuldade para se defender das doenças. No final da vida, o coração deixa de bater, o cérebro e os demais órgãos deixam de funcionar.
Qual a diferença entre cobras e serpentes?
É comum chamar a todos os animais Ofídios (que não tem membros, são répteis) cobras. Mas essa designação está incorreta. Existe uma espécie de ofídios que tem o nome de Naja e que se denomina por cobra. Todas as outras espécies são chamadas de serpentes. Este erro é comum nos portugueses, pois quando estes chegaram ao Brasil, encontraram as serpentes, e chamaram-nas de cobras, assim como nomearam de índios os seus habitantes, pois acreditaram primeiramente terem chegado à Índia.
Em alguns países, cobra é uma palavra usada somente para falar das najas, encontradas na África e na Ásia.
Naja
Por que as formigas se deslocam em fila indiana?
É para não se perder! Andando, a formigas colocam no seu caminho uma substância cheirosa que todas as formigas de uma mesma família reconhecem. Basta seguir esse caminho cheiroso para voltar para casa!
Por que é que as abelhas fabricam mel?
O mel serve para alimentar as outras abelhas e as larvas que vivem nas colmeias. As colmeias são enormes "fábricas" de mel. Para os apicultores, basta colher essa iguaria tomando cuidado com as picadas!
Um cavalo sofre quando as ferraduras são colocadas?
Os cascos dos cavalos são de queratina, uma proteína bem dura, de que também são feitos os chifres dos bois e as nossas unhas. Por isso, o cavalo não sofre quando as ferraduras são colocadas, pelo menos não mais do que quando cortamos as unhas!
Qual é a maior baleia do mundo?
É a baleia-azul. Adulta pode medir 30 metros de comprimento! No entanto, ela só come animais minúsculos. Se não for caçada pode viver mais de 50 anos.
Por que as baleias expelem grande jatos de água?
As baleias podem mergulhar quase meia hora prendendo a respiração, mas elas são obrigadas a subir para respirar. É o ar que a baleia assopra ao voltar à superfície, misturando com a água, que faz esse jato impressionante.
Todos os tubarões são perigosos?
Existem mais de 350 espécies de tubarão. Algumas são ferozes, mas a maioria é inofensiva. O tubarão-anão mede 20 centímetros. O tubarão-baleia, o maior peixe do mundo, mede 15 metros, mas não é perigoso. Os mais temíveis são o tubarão-branco, o tubarão-tigre, que come tudo que encontra, o tubarão-azul, tubarão martelo...
Qual é a menor ave do mundo?
É o beija-flor, também chamado colibri. Ele alimenta-se do néctar das flores e põe dois ovos do tamanho de pequenas ervilhas! O beija-flor bate as asas a toda velocidade e é capaz de fazer vôos rasantes atingindo mais de 50 quilómetros por hora.
Quais os animais mais antigos?
Os animais passaram do mar à terra há 414 milhões de anos. Os primeiros animais terrestres do mundo incluem dois tipos de centípedes e uma pequena aranha encontrada entre restos de plantas.
Quais os animais mais barulhentos?
O mais barulhento dos animais terrestres é o bugio das Américas Central e do Sul. Os machos possuem uma estrutura óssea na parte superior da traqueia que permitem que o som tão forte. Seus gritos assustadores foram descritos como um misto de latido de cão e zurro de asno, ampliado mil vezes. Os seus gritos podem ser ouvidos até 5 km de distância.
Quais os animais mais fortes?
Em proporção com o seu tamanho, os animais mais fortes são os besouros gigantes, encontrados principalmente nos trópicos. Testes realizados com o besouro-rinoceronte demonstravam que pode suportar no seu dorso 850 vezes o próprio peso. Para efeito de comparação, um homem pode levantar (com um auxílio de suporte) apenas 17 vezes o próprio peso.
Qual o animal com a mordida mais forte?
Um tubarão pardo de 2 m de comprimento pode exercer uma força de 60 Kg entre as suas mandíbulas. Apesar de não terem medido as mordidas de tubarões maiores, como o tubarão branco, deve ser ainda mais forte.
Qual o animal com olfato mais aguçado?
O olfato mais aguçado existente na natureza é o do macho da borboleta imperador que segundo experiências feitas na Alemanha em 1961, pode detetar a substância sexual produzida por uma fêmea virgem à distância de 11 Km, contra o vento. Os recetores localizados nas antenas do macho são tão sensíveis que são capazes de detetar uma única molécula de substância.
Qual o animal com mais venenoso?
Os pequenos e brilhantes sapos das Américas Central e do Sul segregam algumas das toxinas mais mortais conhecidas. A espécie é tão perigosa que os cientistas precisam de usar luvas grossas para manipulá-la, no caso de terem cortes ou arranhões nas suas mãos.
Phyllobates terribilis
MAMÍFEROS
O maior mamífero do planeta é a baleia azul.
Uma baleia fêmea pesando 190 t e medindo 27,6 m de comprimento foi capturada no Atlântico Sul.
- Mais longo
O mais longo exemplar já registado foiuma baleia fêmea medindo 33,58 m que encalhou na praia de Grytvi, Geórgia do Sul, em 1909.
- Maior mamífero terrestre
Em média, os elefantes machos atingem a altura de 3 a 3,7 e pesam de 4 a 7 t. O maior exemplar já registado foi um macho morto a tiros em Macusso, Angola. Deitado de lado, o elefante media 4,16 m em uma linha projetada do ponto mais alto do dorso até a base da pata dianteira, indicando uma altura de 3,96 m quanto em pé. O seu peso foi calculado em mais de 12,24 t.
CARNÍVOROS
- Maior terrestre
O maior carnívoro terrestre é o urso polar, cujos machos pesam de 400 a 600 Kg e medem de 2,4 a 2,6 m do focinho à cauda.
- Mais pesado
Um urso polar com 907 Kg e cerca de 3,5 m do focinho à cauda foi abatido a leste de Kotzebue, Alasca, EUA.
- Menos pesado
A doninha anã possui corpo de 11 a 26 cm, cauda de 1,3 a 8,7 cm e pesa de 30 a 200 g, sendo os menores indivíduos são as fêmeas que habitam a Sibéria e os Alpes.
Por que soluçamos?

O soluço é resultado de uma contração involuntária do diafragma, um fino músculo que separa o tórax do abdómen e que, juntamente com os músculos intercostais externos, é responsável pelo controle da respiração. Os seus movimentos de contração e relaxamento permitem que inspiremos e expiremos o ar e são controlados por um nervo, situado logo acima do estômago.
Os soluços surgem a partir de uma irritação de um nervo, cujas causas podem ser diversas (distensão gástrica pela ingestão de bebidas com gás, deglutição de ar ou alimentação em grande volume; mudanças súbitas da temperatura de alimentos ingeridos; modificações da temperatura corporal, como sauna seguida de duche gelado; ingestão de bebidas alcoólicas; ou até mesmo gargalhadas). Quando ele fica ou é sensibilizado, envia uma mensagem para o diafragma se contrair, o que dispara o soluço.
O característico barulhinho "hic, hic" surge quando ocorre o fecho súbito da glote (abertura superior da laringe, onde se localizam as cordas vocais), produzindo vibração nas cordas vocais.
Como acontece o reflexo da tosse?

Os brônquios e a traqueia são tão sensíveis a um toque leve, que quantidades mínimas de material estranho ou substâncias que causam irritação iniciam o reflexo da tosse. Impulsos nervosos provocam:
- inspiração de até 2,5 litros de ar;
- fecho da epiglote e das cordas vocais para aprisionar o ar no interior dos pulmões;
- contração forte dos músculos abdominais e dos músculos intercostais internos, empurrando o diafragma e provocando aumento rápido de pressão nos pulmões;
- abertura súbita das cordas vocais e da epiglote e liberação do ar dos pulmões sob alta pressão.
Desta forma, o ar que é expelido de forma explosiva dos pulmões para o exterior se move tão rapidamente que carrega consigo qualquer material estranho que esteja presente nos brônquios e na traqueia.
Como acontece o reflexo do espirro?

O reflexo do espirro é muito parecido com o reflexo da tosse, exceto pelo fato de se aplicar às vias nasais, ao invés das vias respiratórias inferiores: o estímulo que inicia o reflexo do espirro é a irritação das vias nasais. Uma série de reações semelhantes às do reflexo da tosse acontece, grandes quantidades de ar passam rapidamente pelo nariz, ajudando, assim, a limpar as vias nasais.
Você sabia que:
- o ar que sai das narinas durante o espirro atinge em média 150 Km/hora?
- ao espirrarmos espalhamos aproximadamente 40 mil gotículas de saliva?
Pois é, por isto o espirro é uma excelente fonte de transmissão de doenças respiratórias.
Porque é impossível espirrar de olhos abertos?

Esclarecendo o mito: não é porque os olhos podem sair da órbita que os fechamos ao espirrar!
Quando uma partícula estranha entra no corpo pelas vias nasais, estimula os receptores locais que avisam o encéfalo que é hora de entrar em ação.
Ao receber a mensagem, o encéfalo reage imediatamente à invasão, gerando uma série de impulso motores que contraem o abdômen, o tórax e o diafragma, até chegar ao nervo facial.
Os reflexos que chegam ao nervo facial também desencadeiam movimentos para expulsar a partícula estranha. Essas contrações atingem diversos músculos da face, incluindo o músculo orbicular, que controla o abrir e o fechar dos olhos. Como resultado de todo esse esforço, fechamos os olhos.
Mitos à Refeição
1. A água à refeição engorda?
FALSO. A água nunca engorda, nem à refeição nem fora dela. A água não fornece nenhum nutriente energético, não contém açúcar, nem gordura, nem proteínas. A percentagem de água presente no corpo humano é de 60%, no caso de haver retenção de água pelo organismo, poderá influenciar o peso. No entanto um indivíduo saudável não faz retenção de líquidos. Esta é uma situação associada a algumas doenças e que deve ser sempre acompanhada pelo médico.
2. Posso Comer toda a fruta que quiser?

FALSO. A fruta contém frutose, um açúcar simples que pode ser consumido diariamente mas sem exagero. A quantidade de fruta recomendada diariamente é de 3 a 4 peças.
3. A sopa engorda?
FALSO. Antigamente a sopa era a base da alimentação dos portugueses e como tal estava adaptada às suas necessidades energéticas. Actualmente o papel da sopa mudou mas as receitas também…
As sopas actuais são sobretudo de legumes e fornecem muito poucas calorias. São uma excelente forma de iniciar o almoço e o jantar e muito adequas para quem quer perder peso.
4. Laranja com leite faz mal?
FALSO. Quando adicionamos alimentos com muita acidez ao leite, este pode coalhar. Muito provavelmente foi neste facto que se baseou o mito. Mas nenhum alimento tem a acidez do estômago. Aí o leite vai forçosamente coalhar, ainda que não seja ingerido com laranjas…
Do ponto de vista nutricional, a laranja é rica em vitamina C e o leite é rico em cálcio. Quando se juntam a nível digestivo a Vitamina C favorece a absorção do cálcio. Por isso uma laranja consumida com leite ou outro derivado são uma combinação excelente.
5. O pão engorda?

6. Não se deve beber água quando se sua após exercício físico intenso?

FALSO. Sempre que se realiza exercício físico intenso há eliminação de grandes quantidades de água que se liberta durante o trabalho muscular para permitir a manutenção da temperatura corporal. Sendo a água o maior constituinte do nosso organismo (60-70% do nosso peso), tem que ser reposta o mais rapidamente possível para evitar a desidratação. Deve ser consumida à temperatura ambiente para não causar eventuais choques térmicos.
Triângulos 25 Sep 2013 12:18 PM (11 years ago)

No nosso dia a dia encontramos imensos triângulos.
Existem dois grupos de triângulos em relação ao comprimento do seus lados e aos seus ângulos internos.
O triângulo retângulo possui três lados com designações especiais. O lado oposto ao ângulo reto chama-se hipotenusa e os lados a ele adjacentes chamam-se catetos.
Propriedades dos triângulos
- Num triângulo ao maior lado opõe-se o maior ângulo e ao menor lado opõe se o menor ângulo, e vice-versa.
- Num triângulo a medida do comprimento de qualquer lado é menor do que a soma das medidas dos comprimentos dos outros dois. A esta propriedade dá-se o nome de desigualdade triangular.
- Num triângulo a altura relativamente ao lado, designado por base, é o segmento de reta que une o vértice oposto à base com o pé da
perpendicular traçada desse vértice para a reta que contém a base.
- O ângulo externo de um triângulo é igual à soma dos ângulos internos que lhe são não adjacentes.
- Num triângulo a soma dos três ângulos externos com vértices distintos é igual a um ângulo giro.
Construção de triângulos
Tendo em conta o comprimento de dois dos lados e um dos ângulos
Tendo em conta o comprimento dos três lados do triângulo
Construir um triângulo equilátero
2º caso: Dois triângulos são iguais quando têm dois lados iguais e o ângulo por eles formado é igual.

TRIÂNGULOS_7
Fazer dobragens em papel! 25 Sep 2013 11:52 AM (11 years ago)

A História de Sadako
Estudantes de mais de 3.000 escolas no Japão e de 9 outros países contribuíram, e em 5 de maio de 1958, o Monumento da Paz das Crianças foi inaugurado no parque da Paz de Hiroshima. Todos os anos no Dia da Paz (06/08) pessoas do mundo inteiro enviam Tsurus de papel para o Parque. As crianças desejam espalhar ao mundo a mensagem esculpida à base do monumento de Sadako:
 Este é nosso Grito
Este é nosso GritoEsta é nossa oração:
Paz no mundo
Sadako onde estiver, saiba que sua mensagem está sendo conhecida no mundo todo, esperamos que seja também cumprida." (extraído do site: http://sites.mpc.com.br/chavemagica/origami.htm)
Ora bem, vamos colocar mãos à obra e fazer alguns "Origamis". Para isso deixo-vos alguns vídeos sobre isso. No fim podem optar por procurar gráficos em outros sites.
Achei a ideia de fazer um abecedário em origami muito interessante e por isso encontrei este site: http://en.origami-club.com/abc/index.html
Para o acompanhar, podem fazer algo que o possa ilustrar, tipo para a letra A, Anjo, B, Banana e assim sucessivamente. Vejam aqui: http://www.pragentemiuda.org/2011/01/alfabeto-ilustrado-em-origami.html
M.d.c. e M.m.c. 31 Jul 2013 12:41 PM (11 years ago)
 Verifica as relações existentes entre o máximo divisor comum e o mínimo múltiplo comum.
Verifica as relações existentes entre o máximo divisor comum e o mínimo múltiplo comum.
Vê o seguinte vídeo:
Circunferência e círculo 23 Jul 2013 12:55 PM (11 years ago)

Vamos de férias! 22 Jul 2013 12:16 PM (11 years ago)

Tive pena pois não obtive, por parte dos meus alunos, um grande interesse em visitar este site. De qualquer forma fico contente que tenha ajudado muitos outros.
Tenho pena de não ter mais tempo para tornar estes cantinhos do saber mais completos, mas tentarei fazer sempre melhor e melhor...

Dia da terra! 22 Apr 2013 3:00 AM (11 years ago)
 Olá caros alunos,
Olá caros alunos,

A partir de 1990, o dia 22 de Abril foi adotado mundialmente como o Dia da Terra, dando um grande impulso aos esforços de reciclagem a nível mundial e ajudando a preparar o caminho para a Cimeira do Rio (1992).
Atualmente, uma organização internacional (REDE DIA DA TERRA) coordena eventos e atividades que celebram este dia.
































.jpg?attredirects%3D0)






.jpg)
.jpg)
.jpg)
.jpg)