Contract Programmer Seeks Job in Cambridge (£500 reward) 22 Sep 2024 10:40 AM (last year)
Anyone in Cambridge need a programmer? I'll give you £500 if you can find me a job that I take.
CV at http://www.aspden.com
I make my usual promise, which I have paid out on several times:
If, within the next six months, I take a job which lasts longer than one month, and that is not obtained through an agency, then on the day the first cheque from that job cashes, I'll give £500 to the person who provided the crucial introduction.
If there are a number of people involved somehow, then I'll apportion it fairly between them. And if the timing conditions above are not quite met, or someone points me at a shorter contract which the £500 makes not worth taking, then I'll do something fair and proportional anyway.
And this offer applies even to personal friends, and to old contacts whom I have not got round to calling yet, and to people who are themselves offering work, because why wouldn't it?
And obviously if I find one through my own efforts then I'll keep the money. But my word is generally thought to be good, and I have made a public promise on my own blog to this effect, so if I cheat you you can blacken my name and ruin my reputation for honesty, which is worth much more to me than £500.
I know all styles of programming and many languages, and can use any computer language you're likely to use as it was intended to be used.
I have a particular facility with mathematical concepts and algorithms of all kinds. I can become very interested in almost any problem which is hard enough that I can't solve it easily.
I have a deserved reputation for being able to produce heavily optimised, but nevertheless bug-free and readable code, but I also know how to hack together sloppy, bug-ridden prototypes, and I know which style is appropriate when, and how to slide along the continuum between them.
I've worked in telecoms, commercial research, banking, university research, chip design, server virtualization, university teaching, sports physics, a couple of startups, and occasionally completely alone.
I've worked on many sizes of machine. I've written programs for tiny 8-bit microcontrollers and gigantic servers, and once upon a time every IBM machine in the Maths Department in Imperial College was running my partial differential equation solvers in parallel in the background.
I'm smart and I get things done. I'm confident enough in my own abilities that if I can't do something I admit it and find someone who can.
I know what it means to understand a thing, and I know when I know something. If I understand a thing then I can usually find a way to communicate it to other people. If other people understand a thing even vaguely I can usually extract the ideas from them and work out which bits make sense.
Clojure Setup from Scratch on a Clean Install of Debian 11 30 Dec 2021 6:19 AM (4 years ago)
I've just installed Debian 11 on an ancient netbook whose hard disk failed, so that seems a chance to find out what
we need to do to make a functioning clojure environment from scratch.
The only changes I've made to my default install are things like getting sudo working and setting the UMASK, my home directory is brand new and empty.
first install clojure
$ sudo apt install clojure
$ clojure
Clojure 1.10.2
user=>
Latest stable according to clojure.org is 1.10.3, so that's really not bad!
and we've got a nice command-line REPL with bracket-balancing and history working
user=> (* 8 8)
64
Ctrl-D kills the REPL
Let's see if we can write a program:
$ cat > hello.clj
#!/usr/bin/env clojure
(println "hello")
^D
$ chmod + x hello.clj
$ ./hello.clj
"hello"
Startup time is quite long on my old netbook, so hello.clj takes 14 seconds to run, but the REPL, although sluggish to start up, actually runs pretty responsively once it has started.
And that's on a dell-mini, a 10 year old netbook that wasn't built for speed when it was new.
So that's a working installation, and you can use any editor to edit scripts and run them from the command line.
So far so good! Actually really impressed.
I can program like that, but I like to run clojure from within emacs, which is always the hard bit of getting any new language to work, so let's install emacs
$ sudo apt install emacs
and run it on our file
$ emacs hello.clj
We get no syntax highlighting, and the file is in 'fundamental mode', so emacs by default doesn't recognise .clj files
M-x package-list-packages
Shows some packages, but nothing clojure related, we need to add the melpa archive.
https://stable.melpa.org/#/getting-started
Suggests adding an incantation to your .emacs file:
So create the file ~/.emacs, and put:
(require 'package)
(add-to-list 'package-archives '("melpa-stable" . "https://stable.melpa.org/packages/") t)
(package-initialize)
in it.
Close emacs (Ctrl-X Ctrl-C) and restart it with:
$ emacs hello.clj
Now we can install clojure-mode
M-x package-refresh-contents
M-x package-install
clojure-mode
Again, close emacs and restart
$ emacs hello.clj
On restart, emacs recognises hello.clj as a clojure file, and syntax highlights it.
Again, this all works well so far. Adding MELPA to emacs is just one of those things you have to do in life.
But programming in clojure is best done with a running REPL, and for this we need CIDER
M-x package-install
cider
Once CIDER is installed, the hello.clj file has a CIDER menu, check that you've got CIDER 1.1.1
because all this stuff is still changing quite quickly, and it's a bit temperamental about version
numbers.
and there's an option to start a REPL
CIDER/Clojure/Start Clojure REPL
It complains 'are you sure you want to run cider-jack-in without a clojure project', which is exactly what I want to do, so I say yes.
I was so hoping this would work...
And it looks like it's doing something sensible, trying to start the system clojure with a command line, but it fails with an incomprehensible error message.
I think the problem is that it's trying to use the relatively new clojure command line tools to start a repl, which would be great, except that Debian hasn't got round to packaging them yet.
There doesn't seem to be a way to just use CIDER to edit and run a program using the system version of clojure.
(Although it does look like the CIDER people have at least tried to make that work, more power to them, and maybe it will work one day when the CLI tools get into debian)
So with a heavy heart, install leiningen and create a project file.
$ sudo apt install leiningen
$ cat > project.clj
(defproject vile "" :dependencies [ [org.clojure/clojure "1.10.2"] ])
and now try:
$ lein repl
That will then download a completely new version of clojure 1.10.2 into a local maven repository and
create a "target" directory full of crap in whatever directory you're in.
and eventually give you a repl
check it works, and then kill it with Ctrl-D
go back into emacs, and go into the hello.clj buffer, and again, try
CIDER/Clojure/Start Clojure REPL
Eventually, up should come a usable clojure REPL in emacs.
Now everything should be working, add (* 8 8) to hello.clj, and put the cursor in the middle of the
expression, and press C-M-x , and you should see the result of the evaluation => 64 display
conveniently in the buffer.
Also try M-. to go to the source code of a function, and M-, to go back to where you were
And there are lots of other lovely things about CIDER and using emacs and lisp together as they were meant to be used, which I will leave you to discover on your own.
Have fun!
-----------------------------------------------------------------------------------
Doing it the hard way:
CIDER's jack-in function is a bit magical for me, but luckily it will tell us what it's doing and which versions it needs:
The crucial line in the REPL startup text is:
;; Startup: /usr/bin/lein update-in :dependencies conj \[nrepl/nrepl\ \"0.8.3\"\] -- update-in :plugins conj \[cider/cider-nrepl\ \"0.26.0\"\] -- repl :headless :host localhost
Which implies that we need [nrepl/nrepl "0.8.3"] as a dependency, and [cider/cider-nrepl "0.26.0"]
as a leiningen plugin, presumably to get leiningen to insert the cider-nrepl middleware to its nrepl
connection
So if we modify our project.clj file to look like:
(defproject vile ""
:dependencies [ [org.clojure/clojure "1.10.2"]
[nrepl/nrepl "0.8.3"] ]
:plugins [ [cider/cider-nrepl "0.26.0"] ])
Then
$ lein repl
will start a command line REPL which also has a network port open with CIDER middleware attached,
and which you can connect to from CIDER with
M-x cider-connect
I prefer this way of doing things, for some reason. I think it feels a bit more solid and comprehensible than having emacs running my clojure process.
Fermat's Christmas Theorem : Fixed Points Come In Pairs 24 Dec 2021 2:12 PM (4 years ago)
#!/usr/bin/env clojure ;; Fermats' Christmas Theorem: Fixed Points Come In Pairs ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;; Here's a bunch of code to make svg files of arrangements of coloured squares. ;; I'm using this to draw the windmills. ;; It's safe to ignore this if you're not interested in how to create such svg files. ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; (require 'clojure.xml) (def squaresize 10) (defn make-svg-rect [i j colour] {:tag :rect :attrs {:x (str (* i squaresize)) :y (str (* j squaresize)) :width (str squaresize) :height (str squaresize) :style (str "fill:", colour, ";stroke:black;stroke-width:1px;stroke-linecap:butt;stroke-linejoin:miter;stroke-opacity:1")}}) (defn adjust-list [rectlist] (if (empty? rectlist) rectlist (let [hmin (apply min (map first rectlist)) vmax (apply max (map second rectlist))] (for [[a b c] rectlist] [(- a hmin) (- vmax b) c])))) (defn make-svg [objects] {:tag :svg :attrs { :version "1.1" :xmlns "http://www.w3.org/2000/svg"} :content (for [[i j c] (adjust-list objects)] (make-svg-rect i j c))}) (defn svg-file-from-rectlist [filename objects] (spit (str filename ".svg") (with-out-str (clojure.xml/emit (make-svg objects))))) (defn hjoin ([sql1 sql2] (hjoin sql1 sql2 1)) ([sql1 sql2 sep] (cond (empty? sql1) sql2 (empty? sql2) sql1 :else (let [xmax1 (apply max (map first sql1)) xmin2 (apply min (map first sql2)) shift (+ 1 sep (- xmax1 xmin2))] (concat sql1 (for [[h v c] sql2] [(+ shift h) v c])))))) (defn hcombine [& sqllist] (reduce hjoin '() sqllist)) (defn svg-file [filename & objects] (svg-file-from-rectlist filename (apply hcombine objects))) (defn orange [n] (if (< n 0) (range 0 n -1) (range 0 n 1))) (defn make-composite-rectangle [h v hsquares vsquares colour] (for [i (orange hsquares) j (orange vsquares)] [(+ i h) (+ j v) colour])) (defn make-windmill [[s p n]] (let [ s2 (quot s 2) is2 (inc s2) ds2 (- is2)] (concat (make-composite-rectangle (- s2) (- s2) s s "red") (make-composite-rectangle (- s2) is2 p n "white") (make-composite-rectangle s2 ds2 (- p) (- n) "white") (make-composite-rectangle ds2 (- s2) (- n) p "green") (make-composite-rectangle is2 s2 n (- p) "green")))) ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;; end of drawing code ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;; and here's some code from the previous posts ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;; code to tell us what number a triple represents (defn total [[s p n]] (+ (* s s) (* 4 p n))) ;; the easy green transform (defn green [[s p n]] [s n p]) ;; and the complicated red transform, which doesn't look so bad once you've got it. (defn red [[s p n]] (cond (< p (/ s 2)) [(- s (* 2 p)) (+ n (- s p)) p] (< (/ s 2) p s) [(- s (* 2 (- s p))) p (+ n (- s p))] (< s p (+ n s)) [(+ s (* 2 (- p s))) p (- n (- p s))] (< (+ n s) p) [(+ s (* 2 n)) n (- p (+ n s))] :else [s p n])) (defn make-thin-cross [n] [1 1 (/ (- n 1) 4)]) (defn victory [[s n p]] (assert (= n p)) (hjoin (make-composite-rectangle 0 0 s s "red") (concat (make-composite-rectangle 0 0 n n "green") (make-composite-rectangle n n n n "green") (make-composite-rectangle 0 n n n "white") (make-composite-rectangle n 0 n n "white")))) ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;; end of code from previous posts ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;; A Christmas Eve Theorem ;; Fixed Points Come In Pairs ;; For any given number of squares, there are only so many ways of arranging them into windmills ;; In fact it's easy to enumerate them all ;; Any given number has only so many factors (defn factors [n] (for [i (range 1 (inc n)) :when (zero? (rem n i))] i)) (factors 12) ; (1 2 3 4 6 12) (factors 100) ; (1 2 4 5 10 20 25 50 100) ;; So it only has so many pairs of factors (defn factor-pairs [n] (for [i (range 1 (inc n)) :when (zero? (rem n i))] [i (/ n i)])) (factor-pairs 12) ; ([1 12] [2 6] [3 4] [4 3] [6 2] [12 1]) (factor-pairs 36) ; ([1 36] [2 18] [3 12] [4 9] [6 6] [9 4] [12 3] [18 2] [36 1]) ;; And there are only so many odd numbers that square to less than a given number (defn odd-numbers-whose-square-is-less-than[n] (for [i (range 1 n 2) :while (< (* i i) n)] i)) (odd-numbers-whose-square-is-less-than 49) ; (1 3 5) (odd-numbers-whose-square-is-less-than 103) ; (1 3 5 7 9) ;; given these functions we can just produce all the possible triples (defn all-triples [m] (apply concat (for [s (odd-numbers-whose-square-is-less-than m)] (for [[p n] (factor-pairs (/ (- m (* s s)) 4))] [s p n])))) (all-triples 5) ; ([1 1 1]) (all-triples 9) ; ([1 1 2] [1 2 1]) (all-triples 13) ; ([1 1 3] [1 3 1] [3 1 1]) (all-triples 49) ; ([1 1 12] [1 2 6] [1 3 4] [1 4 3] [1 6 2] [1 12 1] [3 1 10] [3 2 5] [3 5 2] [3 10 1] [5 1 6] [5 2 3] [5 3 2] [5 6 1]) ;; And these triples come in three kinds ;; The first kind is triples that are fixed points of both the red and green transform ;; [1 1 1] is such a triple (red [1 1 1]) ; [1 1 1] (green [1 1 1]) ; [1 1 1] ;; It's not connected to any other triple. It is a red fixed point and a green fixed point simultaneously. ;; The second kind is triples that are fixed points of one transform, but not the other ;; [1 1 2] is such a triple (red [1 1 2]) ; [1 1 2] (green [1 1 2]) ; [1 2 1] ;; It's connected to one other triple, by the green transform. Let's say it's got a green connection ;; which goes somewhere. ;; [1 2 1] is also such a triple (red [1 2 1]) ; [1 2 1] (green [1 2 1]) ; [1 1 2] ;; Its green connection goes to [1 1 2], to form a two-triple chain with two red fixedpoints on it. ;; [3 1 1] is also such a triple (green [3 1 1]) ; [3 1 1] (red [3 1 1]) ; [1 3 1] ;; but it's a fixed point of the green transform, so it has a red connection going out, which goes to [1 3 1] ;; The third kind of triple isn't a fixed point of either transform ;; [1 3 1] is such a triple (red [1 3 1]) ; [3 1 1] (green [1 3 1]) ; [1 1 3] ;; It has two connections out, one red and one green, ;; And they must go to two different triples, because the red transform changes the size of the red square ;; and the green one doesn't ;; Most triples are of this third kind, they can form links in chains ;; An even number of them can potentially form a loop ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;; Suppose we start off from the first kind of triple. ;; We immediately find two fixed points, one red and one green, and we're done ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;; Suppose we start off from the second kind of triple ;; It will have a link out ;; If we follow that link, then we can't go to a triple of the first kind, because that hasn't got any connections ;; If we go to a triple of the second kind, then we're done, because we'll use up its only ;; connection, and we've formed a complete chain with two fixed points ;; If we go to a triple of the third kind, then we have two triples, and one free connection out ;; Where can that connection go? ;; Not back into the chain we're making, all the connections of those triples are already accounted for. ;; So it must go to another triple and we're in the same situation. ;; We can never have more than one free connection on our chain ;; And we can't go on for ever, because there are only so many triples. ;; So eventually we have to link to another of the first kind of triple, having built a chain that connects ;; two fixed points. ;; A chain that connects two red or two green fixed points must have an odd number of connections ;; A chain that connects a red fixed point to a green fixed point must have an even number of connections ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;; If we start from the third kind of triple, we've got two free connections, and we can attach triples to both of them. ;; But we never get more than two free connections. ;; We can't go on for ever, so we eventually either have to join our two free connections to make a loop, or we ;; have to be part of a chain which connects two fixed points of type 2 ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;; Christmas Eve Theorem ;; Fixed points come in pairs, if you start off from one and follow your links, you'll find another ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;; This immediately implies Fermat's Christmas Theorem ;; Because for every number of the form 4n+1 ;; We can make one, and only one thin cross, a red fixed point ;; The existence of this thin cross implies and is implied by the fact that the number is divisible by one. ;; It can't be part of a loop, by the argument above. And its chain can't go on for ever. ;; So if we follow the transforms, red, green, red, green, red, green ...... ;; Sooner or later we'll hit another fixed point. ;; That other fixed point will be one of: ;; A square ;; A fat cross ;; or ;; A square-bladed windmill ;; If we find a square-bladed windmill, we've also found a way to write our number as the sum of an odd and an even square. ;; If we find a square, then we've shown that our number is itself an odd square ;; And if we find a fat cross, then we've shown that our number has a factorization, of the form s*(s+4n) for some n ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;; Another way of saying that is that although this program is not generally safe to run on arbitrary triples: (defn calculate-orbit ([triple transform] (calculate-orbit triple transform '())) ([triple transform orbit] (let [new (transform triple)] (if ( = new triple) (reverse (cons triple orbit)) (recur new (if (= transform green) red green) (cons triple orbit)))))) ;; Because it might go into an infinite loop, ;; This program *is* safe to run, because starts at a red fixed point and so it must follow a chain and end at another fixed point (defn christmas [n] (calculate-orbit (make-thin-cross n) green)) ;; Let's try it out (christmas 5) ; ([1 1 1]) (apply svg-file "windmills5-1" (map make-windmill (christmas 5))) ;; Here we show that 5 = 2*2 + 1*1 (christmas 9) ; ([1 1 2] [1 2 1]) (apply svg-file "windmills5-2" (map make-windmill (christmas 9))) ; nil ;; 9 = 3*3 (christmas 85) ; ([1 1 21] [1 21 1] [3 1 19] [3 19 1] [5 1 15] [5 15 1] [7 1 9] [7 9 1] [9 1 1]) (apply svg-file "windmills5-3" (map make-windmill (christmas 85))) ;; 85 = 9*9+2*2 (even though it's not prime!) (christmas 201) ; ([1 1 50] [1 50 1] [3 1 48] [3 48 1] [5 1 44] [5 44 1] [7 1 38] [7 38 1] [9 1 30] [9 30 1] [11 1 20] [11 20 1] [13 1 8] [13 8 1] [3 8 6] [3 6 8] [9 6 5] [9 5 6] [1 5 10] [1 10 5] [11 5 4] [11 4 5] [3 12 4] [3 4 12] [5 4 11] [5 11 4] [13 4 2] [13 2 4] [9 15 2] [9 2 15] [5 22 2] [5 2 22] [1 25 2] [1 2 25] [3 2 24] [3 24 2] [7 2 19] [7 19 2] [11 2 10] [11 10 2] [9 10 3] [9 3 10] [3 16 3] [3 3 16]) (apply svg-file "windmills5-4" (map make-windmill (christmas 201))) ;; 201 = 3*(3 + 4*16) = 3*67 ;; You might need to zoom in a bit on that last one, but the program will always work ;; Any number of the form 4n+1 can be either expressed as an odd square plus and even square, or it can be factored. ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;; Merry Christmas Everybody! ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
Christmas Theorem: Some Early Orbits 24 Dec 2021 10:21 AM (4 years ago)
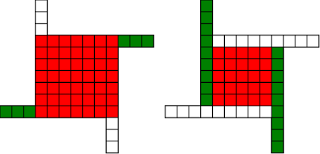
#!/usr/bin/env clojure ;; Fermats' Christmas Theorem: Some Early Orbits ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;; Here's a bunch of code to make svg files of arrangements of coloured squares. ;; I'm using this to draw the windmills. ;; It's safe to ignore this if you're not interested in how to create such svg files. ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; (require 'clojure.xml) (def squaresize 10) (defn make-svg-rect [i j colour] {:tag :rect :attrs {:x (str (* i squaresize)) :y (str (* j squaresize)) :width (str squaresize) :height (str squaresize) :style (str "fill:", colour, ";stroke:black;stroke-width:1px;stroke-linecap:butt;stroke-linejoin:miter;stroke-opacity:1")}}) (defn adjust-list [rectlist] (if (empty? rectlist) rectlist (let [hmin (apply min (map first rectlist)) vmax (apply max (map second rectlist))] (for [[a b c] rectlist] [(- a hmin) (- vmax b) c])))) (defn make-svg [objects] {:tag :svg :attrs { :version "1.1" :xmlns "http://www.w3.org/2000/svg"} :content (for [[i j c] (adjust-list objects)] (make-svg-rect i j c))}) (defn svg-file-from-rectlist [filename objects] (spit (str filename ".svg") (with-out-str (clojure.xml/emit (make-svg objects))))) (defn hjoin ([sql1 sql2] (hjoin sql1 sql2 1)) ([sql1 sql2 sep] (cond (empty? sql1) sql2 (empty? sql2) sql1 :else (let [xmax1 (apply max (map first sql1)) xmin2 (apply min (map first sql2)) shift (+ 1 sep (- xmax1 xmin2))] (concat sql1 (for [[h v c] sql2] [(+ shift h) v c])))))) (defn hcombine [& sqllist] (reduce hjoin '() sqllist)) (defn svg-file [filename & objects] (svg-file-from-rectlist filename (apply hcombine objects))) (defn orange [n] (if (< n 0) (range 0 n -1) (range 0 n 1))) (defn make-composite-rectangle [h v hsquares vsquares colour] (for [i (orange hsquares) j (orange vsquares)] [(+ i h) (+ j v) colour])) (defn make-windmill [[s p n]] (let [ s2 (quot s 2) is2 (inc s2) ds2 (- is2)] (concat (make-composite-rectangle (- s2) (- s2) s s "red") (make-composite-rectangle (- s2) is2 p n "white") (make-composite-rectangle s2 ds2 (- p) (- n) "white") (make-composite-rectangle ds2 (- s2) (- n) p "green") (make-composite-rectangle is2 s2 n (- p) "green")))) ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;; end of drawing code ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;; and here's some code from the previous posts ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;; code to tell us what number a triple represents (defn total [[s p n]] (+ (* s s) (* 4 p n))) ;; the easy green transform (defn green [[s p n]] [s n p]) ;; and the complicated red transform, which doesn't look so bad once you've got it. (defn red [[s p n]] (cond (< p (/ s 2)) [(- s (* 2 p)) (+ n (- s p)) p] (< (/ s 2) p s) [(- s (* 2 (- s p))) p (+ n (- s p))] (< s p (+ n s)) [(+ s (* 2 (- p s))) p (- n (- p s))] (< (+ n s) p) [(+ s (* 2 n)) n (- p (+ n s))] :else [s p n])) ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;; end of code from previous posts ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;; Let's start with the most simple candidate number, 5 = 4.1 + 1 ;; We can always find a thin cross for any number of form 4n+1, almost by definition (defn make-thin-cross [n] [1 1 (/ (- n 1) 4)]) (make-thin-cross 5) ; [1 1 1] ;; [1 1 1] is in fact the only triple that can represent 5, can you see why? (svg-file "windmills4-1" (make-windmill [1 1 1])) ;; This triple is a fixed point of the red transform (crosses always are) (red [1 1 1]) ; [1 1 1] ;; It's also a fixed point of the green transform (because n=p) (green [1 1 1]) ; [1 1 1] ;; It's a fixed point of the green transform because its arms are squares, so I'll call it a square-bladed windmill ;; If we have a square-bladed windmill then we can transform it into an odd and an even square (defn victory [[s n p]] (assert (= n p)) (hjoin (make-composite-rectangle 0 0 s s "red") (concat (make-composite-rectangle 0 0 n n "green") (make-composite-rectangle n n n n "green") (make-composite-rectangle 0 n n n "white") (make-composite-rectangle n 0 n n "white")))) (svg-file "windmills4-2" (victory [1 1 1])) ;; We see that 5 = 1*1 + 2*2 ;; What about the next candidate number up, 9 = 4.2+1 (make-thin-cross 9) ; [1 1 2] ;; again, a red fixed point (because it's a cross) (red [1 1 2]) ; [1 1 2] ;; But not a green one (green [1 1 2]) ; [1 2 1] ;; however that is a fixed point of the red transform, so that's as far as we can go (red [1 2 1]) ; [1 2 1] ;; If we look at this 'orbit' of the triple [1 1 2] as windmills, we see: (apply svg-file "windmills4-3" (map make-windmill '([1 1 2] [1 2 1]))) ;; We see a thin cross, a red fixed point, connected to a square, also a red fixed point ;; We've got two red fixed points connected by the green transform. ;; The square tells us that 9 has a factor, it's not a prime number ;; Let's do the next one (make-thin-cross 13) ; [1 1 3] (red [1 1 3]) ; [1 1 3] ;; crosses are red fixed points (green [1 1 3]) ; [1 3 1] (red [1 3 1]) ; [3 1 1] (green [3 1 1]) ; [3 1 1] ;; We've found a green fixed point, a square-bladed windmill ;; Our orbit is: (apply svg-file "windmills4-4" (map make-windmill '([1 1 3] [1 3 1][3 1 1]))) ;; We've got a red fixed point, connected by a green step and then a red step to a green fixed point (svg-file "windmills4-5" (victory [3 1 1])) ;; The green fixed point gives us our decomposition into odd and even squares ;; 13 = 3*3 + 2*2 ;; The Christmas theorem is looking good so far.... (make-thin-cross 17) ; [1 1 4] ;; cross (green [1 1 4]) ; [1 4 1] (red [1 4 1]) ; [3 1 2] (green [3 1 2]) ; [3 2 1] (red [3 2 1]) ; [1 2 2] (green [1 2 2]) ; [1 2 2] ;; square blades! ;; Our orbit is: (apply svg-file "windmills4-6" (map make-windmill '([1 1 4] [1 4 1][3 1 2] [3 2 1] [1 2 2]))) ;; A red fixed point connected to a green fixed point by four steps. green,red,green,red (svg-file "windmills4-7" (victory [1 2 2])) ;; 17 = 1*1 + 4*4 (make-thin-cross 21) ; [1 1 5] (green [1 1 5]) ; [1 5 1] (red [1 5 1]) ; [3 1 3] (green [3 1 3]) ; [3 3 1] (red [3 3 1]) ; [3 3 1] ;; Our orbit is: (apply svg-file "windmills4-8" (map make-windmill '([1 1 5] [1 5 1][3 1 3] [3 3 1]))) ;; A red fixed point connected to a red fixed point by three steps. green,red,green ;; The red fixed point is a cross. Because the red square is not 1x1, I'm going to call that a 'fat cross' ;; If we have a fat cross, that tells us that our number has a factorization ;; Look: (svg-file "windmills4-9" (concat (make-composite-rectangle 0 0 3 3 "red") (make-composite-rectangle 3 0 1 3 "green") (make-composite-rectangle 4 0 1 3 "white") (make-composite-rectangle 5 0 1 3 "green") (make-composite-rectangle 6 0 1 3 "white"))) ;; In fact, it tells us that 21 = 3*(3+4) = 3*7 ;; The pattern here is that our initial thin crosses (red fixed points) are always connected to other fixed points ;; If the other fixed point is green, it shows us that we have an odd and even square that represent our number ;; If the other fixed point is red, then it shows us that our number has a factor, i.e that it isn't prime. ;; That's the Christmas Theorem. ;; Why would it be true???
Chrismas Theorem: Automatic Windmills 24 Dec 2021 6:20 AM (4 years ago)
#!/usr/bin/env clojure ;; Fermats' Christmas Theorem: Automatic Windmills ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;; Here's a bunch of code to make svg files of arrangements of coloured squares. ;; I'm using this to draw the windmills. ;; It's safe to ignore this if you're not interested in how to create such svg files. ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; (require 'clojure.xml) (def squaresize 10) (defn make-svg-rect [i j colour] {:tag :rect :attrs {:x (str (* i squaresize)) :y (str (* j squaresize)) :width (str squaresize) :height (str squaresize) :style (str "fill:", colour, ";stroke:black;stroke-width:1px;stroke-linecap:butt;stroke-linejoin:miter;stroke-opacity:1")}}) (defn adjust-list [rectlist] (if (empty? rectlist) rectlist (let [hmin (apply min (map first rectlist)) vmax (apply max (map second rectlist))] (for [[a b c] rectlist] [(- a hmin) (- vmax b) c])))) (defn make-svg [objects] {:tag :svg :attrs { :version "1.1" :xmlns "http://www.w3.org/2000/svg"} :content (for [[i j c] (adjust-list objects)] (make-svg-rect i j c))}) (defn svg-file-from-rectlist [filename objects] (spit (str filename ".svg") (with-out-str (clojure.xml/emit (make-svg objects))))) (defn hjoin ([sql1 sql2] (hjoin sql1 sql2 1)) ([sql1 sql2 sep] (cond (empty? sql1) sql2 (empty? sql2) sql1 :else (let [xmax1 (apply max (map first sql1)) xmin2 (apply min (map first sql2)) shift (+ 1 sep (- xmax1 xmin2))] (concat sql1 (for [[h v c] sql2] [(+ shift h) v c])))))) (defn hcombine [& sqllist] (reduce hjoin '() sqllist)) (defn svg-file [filename & objects] (svg-file-from-rectlist filename (apply hcombine objects))) (defn orange [n] (if (< n 0) (range 0 n -1) (range 0 n 1))) (defn make-composite-rectangle [h v hsquares vsquares colour] (for [i (orange hsquares) j (orange vsquares)] [(+ i h) (+ j v) colour])) (defn make-windmill [[s p n]] (let [ s2 (quot s 2) is2 (inc s2) ds2 (- is2)] (concat (make-composite-rectangle (- s2) (- s2) s s "red") (make-composite-rectangle (- s2) is2 p n "white") (make-composite-rectangle s2 ds2 (- p) (- n) "white") (make-composite-rectangle ds2 (- s2) (- n) p "green") (make-composite-rectangle is2 s2 n (- p) "green")))) ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;; end of drawing code ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;; So far so good, but the red transform is a bit manual for my taste. It's easy to see how to do it ;; by eye, but I want to automate that. ;; Let's go over our sequence of shapes for 37 again (svg-file "windmills3-1" (make-windmill [1 1 9]) (make-windmill [1 9 1]) (make-windmill [3 1 7])(make-windmill [3 7 1])(make-windmill [5 1 3])(make-windmill [5 3 1])(make-windmill [1 3 3])) ;; The red transform has a way of flipping the shapes and exchanging the white and green colours, which I'm going to ignore. ;; There may be a more principled way of drawing the triples so that the associated windmills are ;; more consistent with each other, but I don't want to get distracted. I'm already deep down one ;; rabbit hole, and so I'm going to avoid this branch tunnel, or at least save it for later. ;; So, automating the red transform: ;; By eye it's always obvious what to do, but it's not so obvious to a computer, ;; There are actually six different cases to consider, depending on the relative sizes of s, n and p! ;; Let's fix s to be seven, and n to be three, and let p vary, that should be enough to capture all the different cases ;; Start off with p as one, the smallest it can be ;; The picture for the transformation we want to do is: (svg-file "windmills3-2" (make-windmill [7 1 3]) (make-windmill [5 9 1])) ;; We see that the arms of the windmill are all extending into the square, taking squares until they ;; collide with the other arms. ;; Because the arms stay n wide throughout, the collision happens when the arms have all extended by s-n squares. ;; So the normal length 3 gets 6 (7-1) added to it, to become 9, the parallel length 1 stays the same ;; And the red square loses the parallel length taken off it on both sides, so s=7 becomes s=7-2*1 ;; We might think that the transformation would take [7 1 3] to [5 1 9] ;; Or in general terms, s -> s-2p n->n+(s-p), p->p (svg-file "windmills3-3" (make-windmill [7 1 3]) (make-windmill [5 1 9])) ;; But no! During the transformation, the arm that started at the north-west corner extended down so that it's now the arm that ;; starts at the south-west corner, so we need to make our triple with 1 as the normal length and 9 as the parallel length ;; That's what causes the red-green colour flip in our drawings ;; So in fact what we want is s -> s-2p p->n+(s-p), n->p (svg-file "windmills3-4" (make-windmill [7 1 3]) (make-windmill [5 9 1])) ;; In order for this procedure to work, we need s-2p to be positive, or equivalently p < s/2 ;; In code: (defn red [[s p n]] (cond (< p (/ s 2)) [(- s (* 2 p)) (+ n (- s p)) p] :else [s p n])) ;; If the condition's not true, we'll just hand back the original triple (for now...) (red [7 1 3]) ; [5 9 1] (let [[s p n][7 1 3]] (svg-file "windmills3-5" (make-windmill [s p n]) (make-windmill (red [s p n])))) ;; So now let's increase p by one (let [[s p n][7 2 3]] (svg-file "windmills3-6" (make-windmill [s p n]) (make-windmill (red [s p n])))) ;; Looks good, and again (let [[s p n][7 3 3]] (svg-file "windmills3-7" (make-windmill [s p n]) (make-windmill (red [s p n])))) ;; but increasing p again (let [[s p n][7 4 3]] (svg-file "windmills3-8" (make-windmill [s p n]) (make-windmill (red [s p n])))) ;; we see that our idea has failed, that transformation would take up more squares than we have (p > s/2) ;; So we've just given up and returned the original triple ;; Notice that we haven't seen the case where p=s/2, because s is odd, so s/2 isn't an integer ;; If p> s/2, we can do roughly the same thing, but we have to stop earlier. ;; If we imagine our arms extending in, then we'll see that they have to stop after three moves, when they collide with each other ;; that three comes from s-p, so the normal length needs to extend by s-p, and the square needs to lose s-p from both sides ;; And in this case, we don't need to swap n and p, the normal length remains the normal length. ;; The condition for being able to do this is that s-p is positive, or s>p ;; And the transformation is s->s-2(s-p), n->n+(s-p), p->p ;; Adding this case to our transform (defn red [[s p n]] (cond (< p (/ s 2)) [(- s (* 2 p)) (+ n (- s p)) p] (< (/ s 2) p s) [(- s (* 2 (- s p))) p (+ n (- s p))] :else [s p n])) (red [7 4 3]) ; [1 4 6] (let [[s p n][7 4 3]] (svg-file "windmills3-9" (make-windmill [s p n]) (make-windmill (red [s p n])))) ;; In this case, our drawing appears to flip, because the corners of the red square have moved! ;; But we can see that the shape is the same, and the number of squares is the same. ;; keep increasing p (let [[s p n][7 5 3]] (svg-file "windmills3-10" (make-windmill [s p n]) (make-windmill (red [s p n])))) ;; again it works ;; keep increasing p (let [[s p n][7 6 3]] (svg-file "windmills3-11" (make-windmill [s p n]) (make-windmill (red [s p n])))) ;; and again (let [[s p n][7 7 3]] (svg-file "windmills3-12" (make-windmill [s p n]) (make-windmill (red [s p n])))) ;; this time p=s, and so our procedure does nothing. ;; In fact, there's nothing we can do here, we can neither shrink nor expand the red square while keeping the shape the same. ;; I'm going to call this special, more symmetric type of windmill a 'cross'. It's a fixed point of our red ;; transform, we just let it return the same triple. ;; What if we make p even bigger? (let [[s p n][7 8 3]] (svg-file "windmills3-13" (make-windmill [s p n]) (make-windmill (red [s p n])))) ;; Neither of our previous ideas will work, but there's a new option here, we can make the square bigger at the expense of the arms (svg-file "windmills3-14" (make-windmill [7 8 3]) (make-windmill [9 8 2])) ;; Again, the shape appears to flip, but it's just a mirror image of the shape we would get if we extended the red square ;; so how do we code this case? ;; Well, the red square can get bigger (on both sides), by the amount by which the parallel length exceeds the square ;; i.e. p-s ;; The parallel length stays the same, and the normal length goes down by p-s ;; so s-> s+2*(p-s), p->p, n-> n-(p-s) ;; And this should work as long as p-s<n, or p<n+s (defn red [[s p n]] (cond (< p (/ s 2)) [(- s (* 2 p)) (+ n (- s p)) p] (< (/ s 2) p s) [(- s (* 2 (- s p))) p (+ n (- s p))] (< s p (+ n s)) [(+ s (* 2 (- p s))) p (- n (- p s))] :else [s p n])) (red [7 8 3]) ; [9 8 2] (let [[s p n][7 8 3]] (svg-file "windmills3-15" (make-windmill [s p n]) (make-windmill (red [s p n])))) ;; increase p (let [[s p n][7 9 3]] (svg-file "windmills3-16" (make-windmill [s p n]) (make-windmill (red [s p n])))) ;; looks good ;; increase p (let [[s p n][7 10 3]] (svg-file "windmills3-17" (make-windmill [s p n]) (make-windmill (red [s p n])))) ;; Now p=s+n, and we can't make any of our previous ideas work. ;; We could increase the red square to fill the whole shape now, but the result wouldn't be a windmill, and there's nothing ;; else we can do, so we'll leave this case as a fixed point. ;; I'll call this special symmetric windmill a 'square', for obvious reasons. ;; what if p is even larger than s+n? (let [[s p n][7 11 3]] (svg-file "windmills3-18" (make-windmill [s p n]) (make-windmill (red [s p n])))) ;; now there is something we can do, we can increase size of the square by n ;; this takes s+n squares from the parallel length (svg-file "windmills3-19" (make-windmill [7 11 3]) (make-windmill [13 3 1])) ;; Again we need to swap normal and parallel ;; So our final transformation is ;; s-> s+2n, p->n, n-> p-(s+n) ;; And this is the final case, it will work whenever p > n+s (defn red [[s p n]] (cond (< p (/ s 2)) [(- s (* 2 p)) (+ n (- s p)) p] (< (/ s 2) p s) [(- s (* 2 (- s p))) p (+ n (- s p))] (< s p (+ n s)) [(+ s (* 2 (- p s))) p (- n (- p s))] (< (+ n s) p) [(+ s (* 2 n)) n (- p (+ n s))] :else [s p n])) (let [[s p n][7 11 3]] (svg-file "windmills3-20" (make-windmill [s p n]) (make-windmill (red [s p n])))) ;; increase p (let [[s p n][7 12 3]] (svg-file "windmills3-21" (make-windmill [s p n]) (make-windmill (red [s p n])))) ;; increase p (let [[s p n][7 13 3]] (svg-file "windmills3-22" (make-windmill [s p n]) (make-windmill (red [s p n])))) ;; increase p (let [[s p n][7 14 3]] (svg-file "windmills3-23" (make-windmill [s p n]) (make-windmill (red [s p n])))) ;; And we're done, this will work however large p is! ;; That was very fiddly and took me several goes and a bit of paper to get right. But it correctly captures the four different cases that ;; are so easy to do by eye, and also the two cases where it fails, the squares and crosses.
Christmas Theorem: Principled Windmills 22 Dec 2021 7:44 AM (4 years ago)
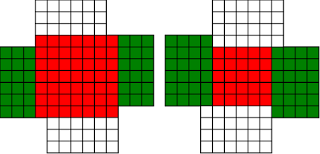
#!/usr/bin/env clojure ;; Fermats' Christmas Theorem: Principled Windmills ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;; Here's a bunch of code to make svg files of arrangements of coloured squares. ;; I'm using this to draw the windmills. ;; It's safe to ignore this if you're not interested in how to create such svg files. ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; (require 'clojure.xml) (def squaresize 10) (defn make-svg-rect [i j colour] {:tag :rect :attrs {:x (str (* i squaresize)) :y (str (* j squaresize)) :width (str squaresize) :height (str squaresize) :style (str "fill:", colour, ";stroke:black;stroke-width:1px;stroke-linecap:butt;stroke-linejoin:miter;stroke-opacity:1")}}) (defn adjust-list [rectlist] (if (empty? rectlist) rectlist (let [hmin (apply min (map first rectlist)) vmax (apply max (map second rectlist))] (for [[a b c] rectlist] [(- a hmin) (- vmax b) c])))) (defn make-svg [objects] {:tag :svg :attrs { :version "1.1" :xmlns "http://www.w3.org/2000/svg"} :content (for [[i j c] (adjust-list objects)] (make-svg-rect i j c))}) (defn svg-file-from-rectlist [filename objects] (spit (str filename ".svg") (with-out-str (clojure.xml/emit (make-svg objects))))) (defn hjoin ([sql1 sql2] (hjoin sql1 sql2 1)) ([sql1 sql2 sep] (cond (empty? sql1) sql2 (empty? sql2) sql1 :else (let [xmax1 (apply max (map first sql1)) xmin2 (apply min (map first sql2)) shift (+ 1 sep (- xmax1 xmin2))] (concat sql1 (for [[h v c] sql2] [(+ shift h) v c])))))) (defn hcombine [& sqllist] (reduce hjoin '() sqllist)) (defn svg-file [filename & objects] (svg-file-from-rectlist filename (apply hcombine objects))) (defn orange [n] (if (< n 0) (range 0 n -1) (range 0 n 1))) (defn make-composite-rectangle [h v hsquares vsquares colour] (for [i (orange hsquares) j (orange vsquares)] [(+ i h) (+ j v) colour])) ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;; end of drawing code ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;; Let's do another example in a more principled way ;; We'll think in terms of triples [s, p, n] ;; Where s is the size of the red square, p (parallel) is the width of the arms , and n (normal) is ;; the length of the arms. ;; Here's a function to draw the windmill that represents such a triple (defn make-windmill [[s p n]] (let [ s2 (quot s 2) is2 (inc s2) ds2 (- is2)] (concat (make-composite-rectangle (- s2) (- s2) s s "red") (make-composite-rectangle (- s2) is2 p n "white") (make-composite-rectangle s2 ds2 (- p) (- n) "white") (make-composite-rectangle ds2 (- s2) (- n) p "green") (make-composite-rectangle is2 s2 n (- p) "green")))) (make-windmill [1 1 1]) ; ([0 0 "red"] [0 1 "white"] [0 -1 "white"] [-1 0 "green"] [1 0 "green"]) (svg-file "windmill" (make-windmill [1 1 1])) ;; As we do our windmill transformations s*s + 4 * p * n should always stay the same (defn total [[s p n]] (+ (* s s) (* 4 p n))) (total [1 1 1]) ; 5 ;; So with this new way of representing things: ;; Consider 37 = 4 * 9 + 1 ;; Our first triple will be [1 1 9] (total [1 1 9]) ; 37 ;; And its windmill looks like: (svg-file "windmill-37-1" (make-windmill [1 1 9]))
;; We can't change the size of the red square here, so the other thing we can do is to rotate the arms ;; In terms of triples, [1 1 9] -> [1 9 1] (total [1 9 1]) ; 37 (svg-file "windmill-37-2" (make-windmill [1 9 1])) ;; Now we can change the size of the red square, it can increase to three, and that means that we have to shorten the arms by two ;; [1 9 1] -> [3 1 7] (total [3 1 7]) ; 37 (svg-file "windmill-37-3" (make-windmill [3 1 7])) ;; Note that this also changes the colour of the arms, but that doesn't matter, the only reason the ;; arms are two different colours is to make it easier to see what's going on. If it bothers you ;; just go and change white to green in the windmill code! ;; From [3 1 7] the only change we can make to the size of the red square is to put it back to one ;; So instead, we'll swap the arms again ;; [3 1 7] -> [3 7 1] (total [3 7 1]) ; 37 (svg-file "windmill-37-4" (make-windmill [3 7 1])) ;; Now, swapping the arms just moves us back a step, but we can increase the size of the red square to five ;; and shorten the arms by two ;; [3 7 1] -> [5 1 3] (total [5 1 3]) ; 37 (svg-file "windmill-37-5" (make-windmill [5 1 3])) ;; Again, the only way to change the size of the red square is to put it back, so let's rotate arms ;; I'm going to call changing the size of the red square the red transformation ;; and rotating the arms the green transformation ;; The green transformation is easy to express in terms of triples (defn green [[s p n]] [s n p]) (green [5 1 3]) ; [5 3 1] (total [5 3 1]) ; 37 (svg-file "windmill-37-6" (make-windmill [5 3 1])) ;; Now, the green transformation just puts us back a step, and it looks like we can't increase the size ;; of the red square, so are we stuck? ;; No! If you stare at the diagram for long enough, you'll see that we can *reduce* the size of the ;; red square instead of increasing it, growing the arms inward until the red shape is square again. ;; And in fact that's our only possible move. ;; [5 3 1] -> [1 3 3] (svg-file "windmill-37-7" (make-windmill [1 3 3])) ;; It's kind of annoying that this flips the shape! But it's obviously still the same total number ;; of squares, so just like with the colour flip I'm going to ignore that for now rather than ;; introduce unnecessary complexity to the drawing code ;; I'm going to call both reducing and increasing the size of the red square a "red transformation", ;; and the red transformation is going to need a parameter to say how much to change the size of the ;; square ;; Let's say, as above, that we want to shift the boundaries of the big red square in by two small unit squares ;; so say delta = -2 ;; that means that the new red square is size one, five less two squares on either edge ;; that means that the red square has changed from size twenty-five to size one ;; that leaves twenty-four spare squares, to be distributed between the four arms ;; which is six spare squares per arm ;; since we're just moving the boundary of the square, or alternatively extending the arms into the ;; square, that doesn't change p, the width of the arm parallel to the square ;; so we add the six squares in rows of p. ;; in our example above, p is three, so those six squares result in the arms lengthening by two ;; In code (defn red [[s p n] delta] (let [news (+ s (* 2 delta)) spare (- ( * s s ) (* news news)) sparesperarm (/ spare 4) lengthchange (/ sparesperarm p)] [news (+ n lengthchange) p])) (total [5 3 1]) ; 37 (red [5 3 1] -2) ; [1 3 3] (total (red [5 3 1] -2)) ; 37 (svg-file "windmill" (make-windmill [5 3 1 ])) ; nil (svg-file "windmill" (make-windmill (red [5 3 1] -2))) ; nil (svg-file "windmill-37-7" (make-windmill [1 3 3]))
;; Now we have a real problem. The only red transformation we can make is to go back a step, but ;; the green transformation does nothing useful here: (green [1 3 3]) ; [1 3 3] ;; But every problem is an opportunity, as they say: ;; We can split up the rectangle (svg-file "windmill-37-split" (make-composite-rectangle 0 0 1 1 "red") (make-composite-rectangle 0 0 3 3 "green") (make-composite-rectangle 0 0 3 3 "green") (make-composite-rectangle 0 0 3 3 "white") (make-composite-rectangle 0 0 3 3 "white")) (svg-file "windmill-37-recombine" (make-composite-rectangle 0 0 1 1 "red") (concat (make-composite-rectangle 0 0 3 3 "green") (make-composite-rectangle 3 3 3 3 "green") (make-composite-rectangle 0 3 3 3 "white") (make-composite-rectangle 3 0 3 3 "white"))) ;; The green transformation fails if and only if the arms are squares, and if the arms are squares, we can ;; combine them to form one big even square (svg-file "windmill-37-final" (make-composite-rectangle 0 0 1 1 "red") (concat (make-composite-rectangle 0 0 6 6 "green"))) ;; So 37 = 1*1 + 6*6 ;; Which is what we're trying to show, thirty-seven is the sum of one odd and one even square
Fermat's Christmas Theorem: Windmills 19 Dec 2021 12:27 PM (4 years ago)
#!/usr/bin/env clojure ;; Fermats' Christmas Theorem: Windmills ;; Sorry for the delay, I had COVID. I'm fine, don't worry! ;; Let's pick an arbitrary number of the form 4n+1, say 29 ;; Precisely because it's of form 4n+1, we can split it into a central square and four identical ;; blocks, in this case, a 1x1 square and four 1x7 blocks ;; 29 = 1*1 + 4 * (1 * 7) (+ (* 1 1) (* 4 (* 1 7))) ; 29 ;; Let's draw that: ;; I'm not going to explain how the svg making thing works, but see: ;; http://www.learningclojure.com/2010/10/generating-xml-to-make-svg-vector.html ;; if you're curious about the details (require 'clojure.xml) (def squaresize 10) (defn make-rect [i j colour] {:tag :rect :attrs {:x (str (* i squaresize)) :y (str (* j squaresize)) :width (str squaresize) :height (str squaresize) :style (str "fill:", colour, ";stroke:black;stroke-width:1px;stroke-linecap:butt;stroke-linejoin:miter;stroke-opacity:1")}}) ;; SVG coordinates have 0,0 in the top left corner, whereas I like my origin in the middle, ;; and with the vertical component increasing as we go up, so this is a coordinate transform ;; That converts my system to SVG's system. (defn adjust-list [rectlist] (let [hmin (apply min (map first rectlist)) vmax (apply max (map second rectlist))] (for [[a b c] rectlist] [(- a hmin) (- vmax b) c]))) (defn make-svg [objects] {:tag :svg :attrs {:width "100%" :height "100%" :version "1.1" :xmlns "http://www.w3.org/2000/svg"} :content (for [[i j c] (adjust-list objects)] (make-rect i j c))}) (defn svg-file [filename objects] (spit (str filename ".svg") (with-out-str (clojure.xml/emit (make-svg objects))))) (defn orange [n] (if (< n 0) (range 0 n -1) (range 0 n 1))) (defn make-composite-rectangle [h v hsquares vsquares colour] (for [i (orange hsquares) j (orange vsquares)] [(+ i h) (+ j v) colour])) ;; With this drawing code in hand we can diagram 29 = 1 * 1 + 4 * (1 * 7) ;; As this windmill shape: (svg-file "windmill-29-1" (concat (make-composite-rectangle 0 0 1 1 "red") (make-composite-rectangle 1 0 7 1 "white") (make-composite-rectangle -1 0 -7 -1 "white") (make-composite-rectangle 0 1 -1 7 "green") (make-composite-rectangle 0 -1 1 -7 "green"))) ;; Or alternatively we could show it as 29 = 1*1 + 4 * (1 * 7) (svg-file "windmill-29-2" (concat (make-composite-rectangle 0 0 1 1 "red") (make-composite-rectangle 1 0 1 7 "white") (make-composite-rectangle -1 0 -1 -7 "white") (make-composite-rectangle 0 1 -7 1 "green") (make-composite-rectangle 0 -1 7 -1 "green"))) ;; Now we notice that there's a 3x3 square in the middle, so what about: (svg-file "windmill-29-3" (concat (make-composite-rectangle -1 -1 3 3 "red") (make-composite-rectangle 1 2 1 5 "white") (make-composite-rectangle -1 -2 -1 -5 "white") (make-composite-rectangle -2 1 -5 1 "green") (make-composite-rectangle 2 -1 5 -1 "green"))) ;; Which is equivalent to 29 = 3*3 + 4* (1 * 5) ;; And then of course we can flatten the arms again: ;; 29 = 3*3 + 4 * ( 5 * 1 ) (svg-file "windmill-29-4" (concat (make-composite-rectangle -1 -1 3 3 "red") (make-composite-rectangle 1 2 -5 1 "white") (make-composite-rectangle -1 -2 5 -1 "white") (make-composite-rectangle -2 1 1 -5 "green") (make-composite-rectangle 2 -1 1 5 "green"))) ;; And we see a 5*5 square now, so ;; 29 = 5*5 + 4 * ( 1 * 1) (svg-file "windmill-29-5" (concat (make-composite-rectangle -2 -2 5 5 "red") (make-composite-rectangle -3 2 -1 1 "white") (make-composite-rectangle 3 -2 1 1 "white") (make-composite-rectangle -2 -3 1 -1 "green") (make-composite-rectangle 2 3 1 1 "green"))) ;; Notice now that our diagram is one big odd square, and four little squares ;; Four little squares can be combined into one big even square ;; 4*1*1 is also equal to 2*2*1*1, = (2*1)*(2*1) = 2*2 ;; so 29 = 5*5+2*2 ;; Which is to say that 29, a prime number of form 4n + 1, is equal to the sum of an odd and an even square. ;; 29 = 25 + 4 ;; These windmill drawings form the core of the proof of the Christmas Theorem. Try the technique out on some other numbers!
A Festive Theorem 3 Dec 2021 1:03 PM (4 years ago)
#!/usr/bin/env clojure ;; A Festive Theorem ;; About a week ago, a friend of mine who is not noted for his interest in pure mathematics, and ;; whose identity I will conceal behind the alias "Sipper" caught me in the Wetherspoons and showed ;; me a number theory proof (or at least most of one, we couldn't actually finish the argument off) ;; I've never been interested in number theory. It seems both useless and boring, but the central ;; idea of this proof was intriguing, so today I sat down, again in Wetherspoons, with quite a lot ;; of paper and coffee and an all-day brunch (all for £7.30, I love Spoons, if you want to advertise ;; on this blog just get in touch), and hammered the damned thing out until I was happy with it. ;; The proof's really visual and beautiful, but not constructive, but it suggested an algorithm to ;; me, so I'm going to try to get that algorithm working, and then show why it works by visualizing ;; what it's doing. ;; I have no idea whether anyone will find this interesting, but since it's the only thing in all of ;; number theory that's ever struck me as worth knowing, and Sips found it interesting too, I'm going ;; to write it up. ;; In this first bit, a statement of the Theorem, which itself took me a while to get my head round. ;; make the repl stop after the first 20 elements of a sequence (set! *print-length* 20) ;; If you square an even number, then it will be divisible by 4 ;; But if you square an odd number, then it will leave a residue of 1 mod 4 (defn square [x] (* x x)) (def mod4 #(rem % 4)) (map mod4 (map square (range))) ;; (0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 ...) ;; If that's not obvious, think about it for a few minutes and see whether you can make it so.... ;; This means that if you take an even and an odd number, and square them, and add the squares, then ;; the residue mod 4 will always be 1 (mod4 (+ (square 2) (square 5))) ;; 1 ( 2*2 + 5*5 = 29 = 28 + 1 = 4 * 7 + 1) (mod4 (+ (square 10) (square 17))) ;; 1 (etc) ;; Let's check this is actually true for lots of numbers: (def naturals (map inc (range))) ;; (1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 ...) (defn odd [n] (- (* 2 n) 1)) (def odds (map odd naturals)) ;; (1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 ...) (defn even [n] (* 2 n)) (def evens (map even naturals)) ;; (2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 ...) ;; Here are all possible pairs of natural numbers (def pairs (for [sum naturals i (take (dec sum) naturals)] (list i, (- sum i)))) ;; ((1 1) (1 2) (2 1) (1 3) (2 2) (3 1) (1 4) (2 3) (3 2) (4 1) (1 5) (2 4) (3 3) (4 2) (5 1) (1 6) (2 5) (3 4) (4 3) (5 2) ...) ;; From which we can construct all odd-even pairs (def odd-even-pairs (for [[i,j] pairs] (list (odd i) (even j)))) ;; ((1 2) (1 4) (3 2) (1 6) (3 4) (5 2) (1 8) (3 6) (5 4) (7 2) (1 10) (3 8) (5 6) (7 4) (9 2) (1 12) (3 10) (5 8) (7 6) (9 4) ...) ;; From which we can construct all sums of squares of odd and even numbers (def odd-even-squares (for [[i,j] odd-even-pairs] (+ (square i) (square j)))) ;;(5 17 13 37 25 29 65 45 41 53 101 73 61 65 85 145 109 89 85 97 ...) ;; paranoid check, if I did that right they should all be 1 mod 4 (map mod4 odd-even-squares) ;; (1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ...) ;; So, since both : it's obvious ; and also it looks like it might actually be true, I think we can take it to the bank that: ;; If o is an odd number, and e is an even number, then o*o+e*e is 1 mod 4 ;; This has apparently been pretty obvious to everyone who's ever thought about it, and is just one ;; of those number-theory facts that always seem to fascinate people who aren't me. ;; But it occurred to Albert Girard in 1632 to wonder if the converse was true: ;; If you have a number that is 1 mod 4, can you always split it into odd and even squares? ;; Let's look for counterexamples: (def early-ones (sort (take 10000 odd-even-squares))) ;; (5 13 17 25 29 37 41 45 53 61 65 65 73 85 85 89 97 101 109 113 ...) (def candidates (map #(+ (* 4 %) 1) naturals)) ;; (5 9 13 17 21 25 29 33 37 41 45 49 53 57 61 65 69 73 77 81 ...) ;; This is such a hack, I am shame.... (require 'clojure.set) (clojure.set/difference (set (take 100 candidates)) (set early-ones)) ;; (9 21 33 49 57 69 77 81 93 105 121 129 133 141 161 165 177 189 201 209 ...) ;; So it looks like the converse is not true. ;; 9, for instance, is 4*2+1, so it's a candidate, but it looks like you can't split it into odd and even squares. ;; Let's try by hand, just going through all the possible odd numbers ;; 9 = 1*1 + 8 ; 8 is not the square of anything ;; 9 = 3*3 + 0 ; 0 is not the square of a natural number ;; This seems a bit dodgy to me, 9 = 3 * 3 + 0 * 0, so does it work if we count 0 as an even number? This will turn out not to matter too much..... ;; Look at 21 ;; 21 = 1*1 + 20 ; 20 is not the square of anything ;; 21 = 3*3 + 12 ; 12 is not the square of anything ;; 21 = 5*5 - 4 ; oops, 5*5 is too big, although it does look like 21 = 5*5 - 2*2, but that wasn't the question. Sum of squares, not difference of squares. ;; OK 33 then ;; 33 = 1*1 + 32 ; 32 is not the square of anything ;; 33 = 3*3 + 24 ; 24 is not the square of anything ;; 33 = 5*5 + 8 ; 8 is not the square of anything ;; 33 = 7*7 - 16 ; oh bloody hell, 33 = 7*7 - 4*4 ;; Anyway, that's not the question. Neither 21 nor 33 are the sum of two squares., even though 21 = 5*4+1 and 33 = 4*8+1 ;; Looking at the list of the ones that did work early-ones ;; (5 13 17 25 29 37 41 45 53 61 65 65 73 85 85 89 97 101 109 113 ...) ;; One might notice that there are an awful lot of prime numbers on that list. (although they're not all primes....) ;; In fact (defn divisors [n] (filter #(= 0 (rem n %)) (map inc (range n)))) (divisors 12) ;; (1 2 3 4 6 12) (defn prime? [n] (= (count (divisors n)) 2)) (filter prime? (range 200)) ;; (2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 ...) (def candidate-primes (filter prime? candidates)) ;; (5 13 17 29 37 41 53 61 73 89 97 101 109 113 137 149 157 173 181 193 ...) (clojure.set/difference (set (take 100 candidate-primes)) (set early-ones)) ;; #{} (clojure.set/difference (set (take 1000 candidate-primes)) (set early-ones)) ;; #{} ;; If there's a prime of form 4*n+1 that isn't the sum of one odd and one even square, then it's fairly big ;; It looks as though, at least for the first thousand candidates, if a number is both prime, and of form 4*n+1, ;; then it is expressible as an even square plus an odd square. ;; Albert Girard, in 1632, presumably after a fair amount of dicking about with bits of paper, ;; conjectured that this might be so for all candidate primes. ;; On December 25th 1640, Pierre de Fermat wrote to his friend Marin Mersenne that he had proved ;; that this was true, but he did not trouble to include the proof or indeed ever tell anyone how he ;; did it. ;; On the 12th of April 1749, Leonhard Euler wrote to his friend Christian Goldbach that he had ;; proved that this was true, and then actually went and published his (intricate and difficult) proof. ;; In recognition of Fermat's invaluable contribution, this result is universally known as ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;; ;; Fermat's Christmas Theorem. ;; ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;; Let p be a prime number ;; Then p is expressible as the sum of odd and even squares ;; if and only if p is 4*n+1 for some natural number n
A test program 2 Dec 2021 10:44 AM (4 years ago)
#!/usr/bin/env clojure ;; It looks like clojure has become a full citizen of Debian ;; In emacs, a syntax highlighted program can be converted to html with htmlize-buffer, and then if ;; you top and tail that and copy it to blogger it comes up nicely. And this seems to still be ;; working after all this time ;; So here is my first published clojure program for a while... ;; If you're using Debian 11, you can run it by installing clojure with ;; $ sudo apt install clojure ;; saving this file as test.clj ;; and then in a terminal window making the file executable ;; $ chmod +x test.clj ;; and then running it ;; $ ./test.clj (println "hello") (defn factorial [n] (if (< n 1) 1 (* n (factorial (- n 1))))) (println '(factorial 10) (factorial 10)) ;; If all is working then you should see something like ;; $ ./test.clj ;; hello ;; (factorial 10) 3628800
Emacs, even 2 Dec 2021 10:27 AM (4 years ago)
The truly terrifying bit of getting any language to work on your machine is getting it to work with EMACS.
Last time I tried to get clojure working, this was the stage that I gave up at. Everything was just broken, and so I wrote the program I was going to write in python instead.
But all it took this time was:
(Emacs 27.1, the version that comes with Debian 11/Bullseye)
M-x package install
clojure-mode
(churn)
and then I can load my test.clj program from earlier, and it's syntax highlighted.
M-x package-list-packages
tells me that it's clojure-mode 5.13.0, from melpa-stable .
I can save the program, and run
./test.clj
from the command line in a terminal, and it just works, with a slightly irritating 2 second delay.
I might hope for more:
I remember once I could do things like putting the cursor in an expression and pressing Alt-Ctrl-x to evaluate that expression in a running REPL.
but this will do for now.
I can always copy and paste things to a REPL, after all.
Clojure Shell Scripts on Debian 2 Dec 2021 9:27 AM (4 years ago)
So I managed to install a very recent clojure through Debian's package manager, and it just worked.
And my next thought is: "If it's somehow become a proper part of Debian, does that mean I can do shell scripts?"
so
cat >test.clj
#!/usr/bin/env clojure
(print "hello")
chmod +x test.clj
./test.clj
(2 second pause...)
hello
Compare with the python equivalent:
#!/usr/bin/env python
print("hello")
chmod +x test.py
./test.py
hello
The only difference is the lack of a two second pause. Python responds instantly.
I can live with a two second pause.
I am totally amazed and pleased by this. It feels much more like a proper programming language than it used to. It's too good to be true.
I wonder if we've got a command line argument parser yet.
Hello Again World (2nd December 2021) Setting Up Clojure on Debian 11 2 Dec 2021 9:12 AM (4 years ago)
It's been a while since I've used Clojure, and I've upgraded my system a fair bit since then, so I'm going to try to start again from scratch.
My computer is running latest stable Debian
cat /etc/debian_version
11.1
(version 11.1, aka bullseye)
My first instinct is to install via the package manager:
apt search clojure
clojure/stable,now 1.10.2-1 all
Lisp dialect for the JVM
clojure.org tells me that the latest version is 1.10.3, so the debian version will do.
sudo apt install clojure
clojure
Clojure 1.10.2
user=>
That seems far too easy, does it work?
First, can I do hello world at all?
user=> (print "hello")
hellonil
user=> (defn factorial [n] (if (< n 2) n (* n factorial (- n 1))))
#'user/factorial
user=> (factorial 10)
Execution error (ClassCastException) at user/factorial (REPL:1).
class user$factorial cannot be cast to class java.lang.Number (user$factorial is in unnamed module of loader clojure.lang.DynamicClassLoader @56ccd751; java.lang.Number is in module java.base of loader 'bootstrap')
Oh my God, what???
.....stares in bewildered disbelief and starts cursing Java and its pointless verbose complexity before seeing the problem and feeling silly...
user=> (defn factorial [n] (if (< n 2) n (* n (factorial (- n 1)))))
#'user/factorial
user => (factorial 10)
3628800
So that looks great, and it was very easy. Things have improved hugely since I last tried this!
I could hope for better error messages, something like 'can't multiply a number by a function' would have been more helpful.
The Unexpected Appearance of Schlemiel, the Painter 5 Feb 2019 6:36 AM (6 years ago)
;; The Unexpected Appearance of Schlemiel, the Painter ;; I was doing some statistics one day, and I defined: ;; the average of a finite sequence (defn average [sq] (/ (reduce + sq) (count sq))) ;; and the square of a number (defn square [x] (* x x)) ;; and a way of forgetting about all the fiddly little digits at the end (defn twosf [x] (float (/ (Math/round (* x 100.0)) 100))) ;; but for the variance I was a little torn between: (defn variance-one [sq] (let [av (average sq)] (average (map #(square (- % av)) sq))))
;; and
(defn variance-two [sq] (let [sqdiff #(square (- % (average sq)))] (average (map sqdiff sq)))) ;; and (I have a regrettable weakness for the terse...) (defn variance-one-liner [sq] (average (map #(square (- % (average sq))) sq))) ;; but I was surprised when I noticed this: (let [s (repeatedly 1000 #(rand))] (twosf (reduce + s)) ;; just to force the sequence to be generated before timing things [(time (twosf (reduce + s))) (time (twosf (average s))) (time (twosf (variance-one s))) (time (twosf (variance-two s))) (time (twosf (variance-one-liner s)))]) ;; "Elapsed time: 0.535715 msecs" ;; "Elapsed time: 0.834523 msecs" ;; "Elapsed time: 1.417108 msecs" ;; "Elapsed time: 251.650722 msecs" ;; "Elapsed time: 248.196331 msecs" ;; [496.83 0.5 0.09 0.09 0.09] ;; It seems that all these functions are correct, in the sense that they are producing ;; correct-looking answers, and yet one of them is orders of magnitude faster. ;; What is going on here, and why?
Reinforcement Learning : Exploration vs Exploitation : Multi-Armed Bandits 13 Dec 2018 1:06 PM (7 years ago)
;; Reinforcement Learning : Exploration vs Exploitation : Multi-Armed Bandits ;; I'm reading the excellent: ;; Reinforcement Learning: An Introduction ;; by Richard S. Sutton and Andrew G. Barto ;; The book's website, on which is available a complete pdf, is here: ;; http://www.incompleteideas.net/book/the-book.html ;; In Chapter 2, they introduce multi-armed bandits as a simplified model problem ;; On the basis that you don't understand anything you can't explain to a computer, I thought I'd code it up: ;; Here is a 2 armed bandit (defn bandit [action] (case action :arms? [:right :left] :right (if (< (rand) 0.5) 4 0) :left (if (< (rand) 0.2) 5 0) :oops!!)) ;; We can ask it how many arms it's got, and what they're called (bandit :arms?) ; [:right :left] ;; And we can pull those arms. Rewards are variable. (bandit :right) ; 4 ; 4 ; 4 ; 0 ; 0 ; 0 ; 0 (bandit :left) ; 5 ; 0 ; 0 ; 0 ; 5 ; 0 ; 5 ; 0 ;; Once we pull an arm, we'll have an action/reward pair (bandit :right) ; 4 ;; the pair would be: [:right 4] ;; Here's a function that yanks an arm at random, and gives us such a pair (defn random-yank [bandit] (let [a (rand-nth (bandit :arms?))] [a (bandit a)])) (random-yank bandit) ; [:left 0] (random-yank bandit) ; [:right 4] ;; And a utility function to take the average of a sequence. We need to be able to provide a default value if the sequence is empty. (defn average ([seq default] (if (empty? seq) default (/ (reduce + seq) (count seq)))) ([seq] (average seq 0))) ;; with some examples (average [1 2 3 4 5]) ; 3 (average (list) 10) ; 10 (average (list 1) 2) ; 1 (average [] 100) ; 100 ;; If we just pull arms at random we get an average reward of about 1.5 (float (average (map second (repeatedly 1000 #(random-yank bandit))))) ; 1.49 ;; Since we can see the code for this particular bandit, we know that ;; the expected value of pulling the right arm is 2 (a half-chance of ;; a reward of 4) and the expected reward for the left arm is 0.2*5 = 1 ;; So if we were seeking to maximize reward, we'd probably be best to pull the right arm all the time. (float (average (map bandit (repeat 10000 :right)))) ; 1.9912 (float (average (map bandit (repeat 10000 :left )))) ; 0.985 ;; The interesting question is, if we don't know how the bandit works, how should we design an algorithm that gets the most reward? ;; (Or at least do better than yanking arms at random!) ;; One thing our algorithm is going to have to do is keep some state to record what happens. ;; Let's start by recording the results of all pulls to date: ;; At first, we know nothing, so we can set up a table to represent that we know nothing (defn initial-state [bandit] (into {} (for [k (bandit :arms?)] [k (list)]))) ;; We haven't pulled either arm yet (initial-state bandit) ; {:right (), :left ()} ;; When we get a new action reward/pair, we'll add the result to our state (defn update-state [state [action reward]] (update-in state [action] #(conj % reward))) ;; here are some examples of using update-state (update-state {:right (), :left ()} [:right 2]) ; {:right (2), :left ()} (reduce update-state {:right (), :left ()} [[:right 2] [:left 3] [:right 4] [:right 5]]) ; {:right (5 4 2), :left (3)} ;; here's how we can use it to record the result of ten random yanks (reduce update-state (initial-state bandit) (repeatedly 10 #(random-yank bandit))) ; {:right (4 4 0 0 0), :left (0 0 0 0 5)} ;; Once we actually have some data, we can make estimates of the expected rewards ;; mapvals applies a function to every value in a map, returning a new map with the same keys (defn mapvals [m f] (into {} (for [[k v] m] [k (f v)]))) ;; examples (mapvals {} inc) ; {} (mapvals {:a 1} inc) ; {:a 2} (mapvals {:a 1, :b 2} inc) ; {:a 2, :b 3} (mapvals {:a 1, :b 2, :c 3} #(* % %)) ; {:a 1, :b 4, :c 9} ;; In the book, Q_t(a) is the current estimate (at time t) ;; We'll use as our estimate of the value of an action the average value seen so far, or zero if we have no information (defn Q [state] (mapvals state #(average % 0))) ;; examples (Q '{:right (5 4 2), :left (3)}) ; {:right 11/3, :left 3} (Q '{:right (5 4 2), :left ()}) ; {:right 11/3, :left 0} (Q (initial-state bandit)) ; {:right 0, :left 0} (Q (update-state (initial-state bandit) (random-yank bandit))) ; {:right 0, :left 2} ;; let's check that we get roughly what we expect in the long run (Q (reduce update-state (initial-state bandit) (repeatedly 10000 #(random-yank bandit)))) ; {:right 9832/5015, :left 1027/997} ;; If we have estimates of the value of each arm, then a good way to ;; use them is to pull the arm with the highest estimate. ;; This is called 'exploitation', as opposed to 'exploration', which ;; is when you try things you think may be suboptimal in order to get ;; information ;; The 'greedy' action is the one with the highest expected value. Of ;; course there may be more than one greedy action especially at first. ;; To help with this, another utility function: ;; max-keys finds the keys with the highest value in a map, and returns a list with just these keys and values (defn max-keys [m] (let [slist (reverse (sort-by second m)) [_ max] (first slist)] (take-while #(= (second %) max) slist))) ;; examples (max-keys {}) ; () (max-keys {1 0}) ; ([1 0]) (max-keys {1 0, 2 0}) ; ([2 0] [1 0]) (max-keys {1 0, 2 1}) ; ([2 1]) (max-keys {1 0, 2 1, 3 -1 , 4 -3, 5 2, 6 2}) ; ([6 2] [5 2]) ;; if there is a tie for the greedy action, we can choose at random between the candidates ;; And so we can go from estimates to greedy action like this: (defn greedy-action [estimates] (first (rand-nth (max-keys estimates)))) ;; examples (greedy-action '{:right 10, :left 3}) ; :right (greedy-action '{:right 10, :left 3 :centre 20}) ; :centre (greedy-action '{:right 10, :left 3 :centre 3}) ; :right (greedy-action '{:right 3, :left 3 :centre 3}) ; :right (greedy-action (Q '{:right (5 4 2), :left (3)})) ; :right (greedy-action (Q '{:right (), :left (3)})) ; :left (greedy-action (Q (initial-state bandit))) ; :left ;; after a lot of random pulls, the greedy action should reliably be the one with the highest expected payoff (greedy-action (Q (reduce update-state (initial-state bandit) (repeatedly 10000 #(random-yank bandit))))) ; :right ;; OK, so we have our stage set, a way of recording what's happened, and some helpful functions defined. ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;; Our first try at a learning algorithm will be 'by hand', as it were. ;; We'll always make the 'greedy' choice. ;; At first, we have no records to go on (initial-state bandit) ; {:right (), :left ()} ;; expected values for both levers are therefore zero (Q (initial-state bandit)) ; {:right 0, :left 0} ;; so the greedy action will get chosen at random (greedy-action (Q (initial-state bandit))) ; :left ;; in this case, we've chosen :left, and the bandit's response is (bandit :left) ; 0 ;; we record it (update-state (initial-state bandit) [:left 0]) ; {:right (), :left (0)} ;; and we have a new state '{:right (), :left (0)} ;; new estimates (Q '{:right (), :left (0)}) ; {:right 0, :left 0} ;; and again, we choose at random (greedy-action (Q '{:right (), :left (0)})) ; :left ;; the bandit is not feeling very generous (bandit :left) ; 0 (update-state '{:right (), :left (0)} [:left 0]) ; {:right (), :left (0 0)} ;; new state: '{:right (), :left (0 0)} ;; new estimates (Q '{:right (), :left (0 0)}) ; {:right 0, :left 0} ;; this time we choose :right (greedy-action (Q '{:right (), :left (0 0)})) ; :right ;; and the bandit pays out! (bandit :right) ; 4 (update-state '{:right (), :left (0 0)} [:right 4]) ; {:right (4), :left (0 0)} ;; the greedy action will be :right now, because we have evidence that right is better. (greedy-action (Q '{:right (4), :left (0 0)})) ; :right ;; You get the idea...... ;; Let's automate that.... ;; Given a state and a bandit, we decide an action and the bandit ;; responds, producing an action/reward pair, and a new state (defn greedy-algorithm [bandit state] (let [action (greedy-action (Q state)) reward (bandit action)] [[action reward] (update-state state [action reward])])) (greedy-algorithm bandit (initial-state bandit)) ; [[:left 0] {:right (), :left (0)}] ;; To get something we can iterate: (defn step [[[a r] state]] (greedy-algorithm bandit state)) (iterate step [ [:dummy :dummy] (initial-state bandit)]) ;; ([[:dummy :dummy] {:right (), :left ()}] ;; [[:left 5] {:right (), :left (5)}] ;; [[:left 0] {:right (), :left (0 5)}] ;; [[:left 0] {:right (), :left (0 0 5)}] ;; [[:left 0] {:right (), :left (0 0 0 5)}] ;; [[:left 0] {:right (), :left (0 0 0 0 5)}] ;; [[:left 0] {:right (), :left (0 0 0 0 0 5)}] ;; [[:left 0] {:right (), :left (0 0 0 0 0 0 5)}] ;; [[:left 0] {:right (), :left (0 0 0 0 0 0 0 5)}] ;; [[:left 0] {:right (), :left (0 0 0 0 0 0 0 0 5)}] ;; [[:left 0] {:right (), :left (0 0 0 0 0 0 0 0 0 5)}] ;; [[:left 0] {:right (), :left (0 0 0 0 0 0 0 0 0 0 5)}] ;; [[:left 5] {:right (), :left (5 0 0 0 0 0 0 0 0 0 0 5)}] ;; [[:left 0] {:right (), :left (0 5 0 0 0 0 0 0 0 0 0 0 5)}] ;; [[:left 0] {:right (), :left (0 0 5 0 0 0 0 0 0 0 0 0 0 5)}] ;; [[:left 0] {:right (), :left (0 0 0 5 0 0 0 0 0 0 0 0 0 0 5)}] ;; [[:left 0] {:right (), :left (0 0 0 0 5 0 0 0 0 0 0 0 0 0 0 5)}] ;; In this case, the greedy algorithm happens to get a payout on its ;; first try, and decides that it will pull that arm for ever. It ;; never even tries the other arm. ;; Try again: (iterate step [ [:dummy :dummy] (initial-state bandit)]) ;;([[:dummy :dummy] {:right (), :left ()}] ;; [[:right 0] {:right (0), :left ()}] ;; [[:right 0] {:right (0 0), :left ()}] ;; [[:left 0] {:right (0 0), :left (0)}] ;; [[:right 4] {:right (4 0 0), :left (0)}] ;; [[:right 4] {:right (4 4 0 0), :left (0)}] ;; [[:right 4] {:right (4 4 4 0 0), :left (0)}] ;; [[:right 4] {:right (4 4 4 4 0 0), :left (0)}] ;; [[:right 4] {:right (4 4 4 4 4 0 0), :left (0)}] ;; [[:right 4] {:right (4 4 4 4 4 4 0 0), :left (0)}] ;; [[:right 0] {:right (0 4 4 4 4 4 4 0 0), :left (0)}] ;; [[:right 0] {:right (0 0 4 4 4 4 4 4 0 0), :left (0)}] ;; [[:right 4] {:right (4 0 0 4 4 4 4 4 4 0 0), :left (0)}] ;; [[:right 0] {:right (0 4 0 0 4 4 4 4 4 4 0 0), :left (0)}] ;; [[:right 4] {:right (4 0 4 0 0 4 4 4 4 4 4 0 0), :left (0)}] ;; [[:right 0] {:right (0 4 0 4 0 0 4 4 4 4 4 4 0 0), :left (0)}] ;; In this case, it tried the right arm a couple of times, then had a ;; go with the left arm, then went back to the right arm, won a ;; payout, and then got hung up on pulling the right arm repeatedly. ;; We've got a couple of problems here! ;; First is that the algorithm has clearly got into a state where it ;; always pulls the left arm (in the first case), and the right ;; arm (in the second case). ;; It can't be doing the right thing in both cases. ;; Secondly the state is growing linearly, as the algorithm remembers ;; all previous results. That's giving us algorithmic complexity ;; problems and the calculation will get slower and slower, and ;; eventually run out of memory.
Define Macro 6 Dec 2015 8:23 AM (10 years ago)
;; When I say (def a (* 4 5)) ;-> #'user/a ;; I'd rather the repl told me that I'd just assigned the value 20 to ;; something rather than that I'd just assigned something to user/a a ;-> 20 ;; A macro for this is easy (defmacro define [var expr] `(let [tmp# ~expr] (def ~var tmp#) tmp#)) (define a (* 4 5)) ;-> 20 ;; I'd also like to be able to say, in a scheme-like manner '(define (square x) (* x x)) ;; meaning (defn square [x] (* x x)) ; #'user/square ;; So I can modify my define macro so: (defmacro define [var expr] (cond (symbol? var) `(let [tmp# ~expr] (def ~var tmp#) tmp#) (list? var) `(defn ~(first var) ~(into [] (rest var)) ~expr))) (macroexpand '(define a (* 20 20))) ;-> (let* [tmp__1986__auto__ (* 20 20)] (def a tmp__1986__auto__) tmp__1986__auto__) (macroexpand '(define (square x) (* x x))) ;-> (def square (clojure.core/fn ([x] (* x x)))) (define a (* 20 20)) ; 400 (define (cube x) (* x x x)) ;-> #'user/cube (cube 20) ;-> 8000 ;; I must say, I haven't actually tried this in practice yet, but it looks like it might work (define (random-error) (+ (rand) -0.5)) ;-> #'user/random-error (random-error) ;-> -0.28442993770155234 (random-error) ;-> 0.2911519817783499 (random-error) ;-> -0.4037254523155406 (define bell (/ (reduce + (repeatedly 10 random-error)) 10)) ;-> 0.015416035491431623 ;; I'm sure someone will let me know if it's broken. ;; This is a bit sub-optimal: (define square (fn[x] (* x x))) ; #function[user/eval8586$tmp--8558--auto----8587] ;; Any suggestions for improvements?
An Introduction to the Lambda Calculus 22 Nov 2015 7:30 AM (10 years ago)
;; Done Twice as a "Dojo" at Villiers Park on Thursday 19th March 2015 ;; To groups of about 15 ultra-clever teenagers who were thinking about doing Computer Science at university ;; The first group got as far as higher order functions in an hour. ;; The second group went a bit faster, and we had a bit more time, about an hour and a half, ;; and so we got right to iterative-improve and finding square roots of anything using it. ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;; Environment DrRacket (version 6.1) ;; Language R5RS (Revised Revised Revised Revised Revised Report on the Algorithmic Language Scheme) ;; One person sits at the computer, one person helps them, the rest tell them what to do ;; Every time they achieve something significant, rotate audience->copilot->pilot->audience ;; Notes on back of hand: (define crib '( 2 3 + (+ 2 3) lambda define square < #t #f if abs Heron average improve make-improver error good-enough good-enough-guess iterative-improve )) ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;; Introduction to the Lambda Calculus ;; More precisely, an introduction to the algorithmic language Scheme, which is what you get if you start with ;; the lambda calculus and you trick it out with some extra stuff that often comes in handy, true and false and if ;; and define and also some types of numbers, like integers and fractions, and adding, and multiplying. ;; You can build all that stuff starting from scratch with just lambda, and it's a nice thing to do if you want ;; to understand how it all works, but I reckon you're already ok at that sort of thing. ;; So we'll start from something that can do basic arithmetic, and we'll learn how to find square roots of things. ;; This is an evaluator. You can ask it the values of things. 2 3 + ;; We can apply the procedure to the two numbers (+ 2 3) ;; Can you tell me the square of 333? (* 333 333) ;; The brackets mean (work out the value of the things in the brackets, and then do the first thing to the other things) ;; So what do you get if you add the squares of 3 and 4? (+ (* 3 3) (* 4 4)) ;; We have procedures for * and + , but if we ask the evaluator what & means, or what square means ;; it will just say 'I have no clue'. ;; It might be nice if we had a procedure for squaring things ;; How you make a procedure is with this thing called lambda, which is sort of a rewriting sort of thing. ;; Try (lambda (x) (* x x)), which means 'make me a thing which, when I give the thing x, gives me the value of (* x x) instead' (lambda (x) (* x x)) ;; #<procedure>, it says, which is very like what you get when you type in +, and it says #<procedure:+>. ;; So we hope we've made a procedure like + or * ;; How shall we use it to get the square of 333? ((lambda (x) (* x x)) 333) ;; Now obviously, typing out (lambda (x) (* x x)) every time you mean square is not brilliant, ;; so we want to give our little squaring-thing a name. (define square (lambda (x) (* x x))) ;; Now how do we find the square of 333? (square 333) ; 110889 ;; So lambda is allowing us to make new things, to turn complicated procedures into simple things ;; and define is allowing us to give things names ;; So now let's make a procedure that takes two things, and squares them both, ;; and adds the squares together, and let's call it pythag (define pythag (lambda (x y) (+ (square x) (square y)))) (pythag 3 4) ;; OK, great, now can you figure out how the procedure < works? ( < 3 4) ( < 4 3) ( < 3 4 6) ( < 3 4 2) ;; Notice that these #t and #f things are things that the evaluator knows the value of: ;; They're called true and false. #f #t ;; So now the last piece of the puzzle: ;; if takes three things: (if #t 1 2) ;1 (if #f 1 2) ;2 ;; So we've got numbers and *,+,-,/, and we've got #t #f and if, and we've got lambda, and define ;; And so all the stuff we've got above, we can think of it as a reference manual for a little language. ;; We can build the whole world out of this little language. ;; That's what God used to build the universe, and any other universes that might have come to His mind. ;; And we can use it too. ;; Here's the manual 2 * (* 2 3) (define forty-four 44) forty-four (lambda (x) (* x x)) ((lambda (x) (* x x)) 3) (if (< 2 3) 2 3) ;; And if we understand these few lines, then we understand the whole thing, and we can fit the little pieces together like this: (define square (lambda (x) (* x x))) (square 2) ;; So now I want you to use the bits to make me a function, call it absolute-value, which if you give it a number gives you back ;; the number, if it's positive, and minus the number, if it's negative. (define absolute-value (lambda (x) (if (> x 0) x (- x)))) (absolute-value 1) (absolute-value -3) (absolute-value 0) ;; So I've taught you most of the rules for Scheme, which is a sort of super-advanced lambda calculus, and so if you understand ;; the bits above, then you've got the hang of the lambda calculus plus some more stuff. ;; And it's a bit like chess. The rules of chess are super-simple, you can explain them to babies, ;; like Dr Polgar did to Judit and her sisters. ;; But that doesn't make the babies into good chess players yet. They have to practise. ;; How are we doing for time? We've done the whole of the lambda calculus, plus some extra bits. We should feel pretty smug. ;; (In both cases, this had taken about 35 minutes) ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;; Let's do a little practice exercise. Like a very short game of chess, now I've explained most of the rules. ;; So once upon a time there was this guy, believe it, called 'Hero of Alexandria'. ;; Or sometimes he seems to have been called 'Heron of Alexandria', like Hero was the short version, ;; like he was sometimes called Jack and sometimes called John. ;; Whatever, Hero invented the syringe, and the vending machine, and the steam engine, and the windmill, and the rocket, ;; and the shortest path theory of reflection of light, and did some theatre stuff, ;; and he was like Professor of War at the big library in Alexandria. ;; You get the impression that if Alexandria had lasted just a little bit longer, ;; the whole industrial revolution would have kicked off right there, and the Romans would have walked on the moon in about AD400. ;; And we'd all be immortal, and live amongst the stars. So you should take the fall of the Roman Empire *very* personally. ;; And one of his things was a way of finding the square roots of numbers, ;; which is so good that it was how people found square roots right up until the invention of the computer. ;; So I'm going to explain that method to you, and you're going to explain it to this computer, and then you can get the computer ;; to calculate square roots for you, really fast. And after that you're only a couple of steps away from cracking the ;; Enigma codes and winning the second world war and inventing the internet and creating an artificial intelligence ;; that will kill us all just 'cos it's got better things to do with our atoms. I'm not joking. ;; So careful.... What I've just given you is the first step on the path that leads to becoming a mighty and powerful wizard. ;; And with great power comes great something or other, you'll find it on the internet, so remember that. ;; PAUSE ;; So imagine you want to find the square root of 9. And you're a bit stuck, so you say to your friend, "What's the square root of nine?", and he says it's three. ;; How do you check? (* 3 3) ;; Bingo. There's another way to check (/ 9 3) ;; That's what it means to be the square root of something. If you divide the something by the square root, you get the square root back. ;; But what if your friend had said "err,.. 2 or something?" (/ 9 2) ;; Notice that the number you put in is too low, but the number you got back is too high. ;; So Heron says, let's take the average. ;; So we need an average function (define average (lambda (a b) (/ (+ a b) 2))) (average 2 (/ 9 2)) ; 3 1/4 ;; three and a quarter, that's like a much better guess, it's like you'd found a cleverer friend. ;; so try again. (average 3.25 (/ 9 3.25)) ; 3.009615... ;; and again (average 3.0096 (/ 9 3.0096)) ; 3.0000153.. (average 3.0000153 (/ 9 3.0000153)) ; 3.000000000039015 ;; So you see this little method makes guesses at the square root of nine into much better guesses. ;; We see that this is kind of a repetitive type thing, and if you see one of those, your first thought should be, ;; I wonder if I can get the computer to do that for me? ;; Can you make a function which takes a guess at the square root of nine, and gives back a better guess? (define improve-guess (lambda (guess) (average guess (/ 9 guess)))) ;; I'd better show you how to format these little functions so that they're easier to read (define improve-guess (lambda (guess) (average guess (/ 9 guess)))) ;; The evaluator doesn't notice the formatting, and it makes it a bit more obvious what's getting replaced by what. (improve-guess 4) ; 3 1/8 (improve-guess (improve-guess 4)) ; 3 1/400 (improve-guess (improve-guess (improve-guess 4))) ; 3 1/960800 ;; We all know what the square root of nine is, let's look at a more interesting number, two. ;; It's a bit of an open question whether 'the square root of two' is a number, or whether it's just a noise ;; that people make with their mouths shortly after you show them a square and tell them about Pythagoras' theorem. ;; Pythagoras used to have people killed for pointing out that you couldn't write down the square root of two. ;; I've got a bit of a confession to make. ;; Someone's already explained to this computer how to find square roots (sqrt 9) ; so far so good! (sqrt 2) ; 1.4142135623730951 hmmm. let's check. (square (sqrt 2)) ; 2.0000000000000004 ;; So it turns out that this guy's just said, if you can't come up with the square root of two, just lie, and come up with something ;; that works, close as dammit. ;; Which is like, bad practice, and tends to lead to Skynet-type behaviour in the long run. ;; So let's see what Hero would have said about it. ;; We need a new function that makes guesses better at being square roots of two. ;; It's a bit dirty, but let's just call that improve-guess as well. ;; That's called redefinition, or 'mutation', and it's ok when you're playing around, ;; but it's a thing you should avoid when writing real programs, because, you know, Skynet issues. ;; Hell, no-one ever got more powerful by refraining from things. (define improve-guess (lambda (guess) (average guess (/ 2 guess)))) ;; Anyone make a guess? (improve-guess 1) ; 1 1/2 ;; Any good? (square (improve-guess 1)) ; 2 1/4 ;; How wrong? (- (square (improve-guess 1)) 2) ; 1/4 ;; OK, I want you to notice that we've just done the same thing twice (define improve-guess-9 (lambda (guess) (average guess (/ 9 guess)))) (define improve-guess-2 (lambda (guess) (average guess (/ 2 guess)))) ;; Now whenever you see that you've done the same thing twice, and there's this sort of grim inevitability ;; about having to do it a third time someday, you should think: ;; Hey, this looks like exactly the sort of repetitive and easily automated task that computers are good at. ;; And so now I want you to make me (and this is probably the hard bit of the talk...) a function which ;; I give it a number and it gives me back a function which makes guesses at square roots of the number better. (define make-improve-guess (lambda (n) (lambda (guess) (average guess (/ n guess))))) ;; And now we can use that to make square root improvers for whatever numbers we like (define i9 (make-improve-guess 9)) (i9 (i9 (i9 (i9 1)))) ; 3 2/21845 (define i2 (make-improve-guess 2)) (i2 (i2 (i2 (i2 1)))) ; 1 195025/470832 ;; The first group got this far in about an hour, which was all we had time for, and then we stopped and I waffled for a bit. ;; Now how good are our guesses, exactly? (- 2 (square (i2 (i2 (i2 (i2 1)))))) ;; We could totally make a function out of that: (define wrongness (lambda (guess) (- 2 (square guess)))) (wrongness (improve-guess 1)) ; -1/4 (wrongness (improve-guess (improve-guess 1))) ; -1/144 (wrongness (improve-guess (improve-guess (improve-guess 1)))) ; -1/166464 (wrongness (improve-guess (improve-guess (improve-guess (improve-guess 1))))) ; -1/221682772224 ;; So we're getting closer! When should we stop? Let's say when we're within 0.00000001 (define good-enough? (lambda (guess) (< (absolute-value (wrongness guess)) 0.00000001))) (good-enough? (improve-guess (improve-guess 1))) ; #f (good-enough? (improve-guess (improve-guess (improve-guess (improve-guess 1))))) ; #t ;; Now, we're doing a bit too much typing for my taste. ;; What we want to do is to say: ;; I'll give you a guess. If it's good enough, just give it back. If it's not good enough, make it better AND TRY AGAIN. ;; This is the hard bit. We need to make a function that calls itself. ;; Go on, have a go (define good-enough-guess (lambda (guess) (if (good-enough? guess) guess (good-enough-guess (improve-guess guess))))) (good-enough-guess 1) ; 1 195025/470832 ;; YAY VICTORY! ;; The second group got this far in about an 1hr 10 mins, but they all still seemed keen and we didn't have to stop, so: ;; Now this is as much of the talk as I'd written, ;; but actually we've got the time to go a little bit further, if your brains haven't totally exploded, and you might like the next bit, ;; because it makes a nice punchline to the whole thing: ;; There's a pattern here, and it's called iterative-improve ;; And iterative improvement is everywhere in the world, for instance you probably got shown the Newton-Raphson solver at school, ;; which is a thing which can find roots of all sorts of equations very fast, and it works like this, you have an initial guess, and ;; Newton Raphson is a way of making a guess into a better guess, and you need to know when the answer is good enough so you can stop. ;; Or this morning I had a shower, and I got in the shower and I turned the water on to just a random position and it was too hot, so I turned the handle ;; a bit the other way and it was a bit too cold, so I turned it back just a bit and then it was ok so I stopped. ;; And that's the same pattern, and you see this sort of thing all over, it is how you solve big matrices and so on and so forth. ;; And we have just discovered this pattern, which is kind of a fundamental building block when you're writing programs, like a for loop is another basic pattern. ;; So let's see if we can make a function that takes a guess and a way of improving guesses and a way to tell if we're done yet, and gives us back an answer. (define iterative-improve (lambda (guess improve good-enough?) (if (good-enough? guess) guess (iterative-improve (improve guess) improve good-enough?)))) (iterative-improve 1 (make-improve-guess 2) good-enough?) ; 1 195025/470832 ;; This was where we stopped the second session. Here's some waffle: ;; And I think now you can see that we've abstracted a pattern here that will come in handy for the sorts of things that we're trying to do. ;; That's what this talk has really been about, how to build a language which allows you to solve the problems that you're interested in. ;; So I'd like to tidy up the program that we've just written, and put it into the sort of form that I'd have written it in, if I'd been solving this problem ;; and I'd played around for a bit and found what I thought was a nice expression of the ideas that we've been talking about. (define square (lambda (x) (* x x))) (define absolute-value (lambda (x) (if (> x 0) x (- x)))) (define make-improve-guess (lambda (n) (lambda (guess) (average guess (/ n guess))))) ; this bit is Heron's method (define make-good-enough? (lambda (n tolerance) (lambda (guess) (> tolerance (absolute-value (- n (square guess))))))) (define iterative-improve (lambda (guess improve good-enough?) (if (good-enough? guess) guess (iterative-improve (improve guess) improve good-enough?)))) (define make-square-root (lambda (guess tolerance) (lambda (n) (iterative-improve guess (make-improve-guess n) (make-good-enough? n tolerance))))) ;; We can use these bits to make the sort of square root we usually find provided: (define engineer-sqrt (make-square-root 1.0 0.00000000000001 )) (engineer-sqrt 2) ;; And here's what we might use, if we needed really good square roots for some reason: (define over-cautious-engineer-square-root (make-square-root 1 1/1000000000000000000000000000000000000000000000000000000000000000000)) (over-cautious-engineer-square-root 2) ;; And I hope you can see this this program is actually built of lots of tiny simple pieces, ;; all of which you can understand, and most of which you'll be able to reuse in other contexts. ;; In particular, iterative-improve is a terribly general thing which you can use in lots of ways. ;; And it might have taken us a while to write, although we wrote it as part of a learning-the-language finger-exercise, ;; but we never have to write it again. It works and it will keep working and we've got in the bank now. ;; Here's the take-home message: ;; If you've got a problem, build yourself a language to solve the problem in. ;; To do that, you need to start with a language that allows you to abstract what you do into simple pieces ;; which are easy to understand, so that you can see that they're right and they aren't too snarled up with ;; the little details of the problem you're working on at the moment. ;; And you need a language that allows you to combine the little pieces easily ;; to make new pieces that solve the problem that you're trying to deal with. ;; And there's a sense in which all computer languages are just this lambda calculus. ;; We've done all this in Scheme, which is lambda calculus plus some extra stuff. ;; There's nothing we've done here that can't be done in python, or in ruby, or in perl or in haskell or in lisp. ;; What distinguishes these languages is what extra stuff has already been added to them. ;; But if a language is good enough, and none of the usual features have actually been taken away, ;; which does happen sometimes, then if there's anything missing that you need you can always add it yourself. ;; And then you can use the language that you have to build the language that you need. ;; In a sense, making languages is itself an iterative improvement process. ;; And the big questions are always: ;; How do we make things better? What's good enough? When are we done? ;; Postscript ;; I'll show you a trick now. We've been using it all along and nobody noticed, ;; but it's the sort of thing that looks like magic, and I don't like magic unless I can cast the spells myself. (good-enough-guess 1) ; 1 195025/470832 (good-enough-guess 1.0) ; 1.4142135623746899 ;; This is called 'contagion'. There are really two types of numbers. ;; Numbers that look like 432/123 are called 'exact', or 'vulgar fractions' ;; Numbers that look like 1.4142 are called 'inexact', or 'approximate', or 'floating point', or 'decimal fractions' ;; The first type are the sort of numbers that children learn about in school, and that mathematicians use. ;; And the second type are the sort of numbers that engineers use, and they're actually quite a lot more complicated and fuzzy ;; than the exact type. They just sort of work like 'if it's very close, then it's good enough'. ;; The way most computers think about them, they keep about sixteen digits around, and if you want more than that, tough luck. ;; But for some purposes they're better, for instance they're easier to read, and it's a bit of a matter of taste. ;; If you multiply or add an inexact number to an exact number, the answer is always inexact. ;; You can't unapproximate something. (/ 1 3) ; 1/3 (/ 1.0 3) ; 0.3333333333333333 ;; We all know that 1/3 isn't really 0.33333333333333 ;; Mathematicians worry about that sort of thing. Engineers don't. Sometimes aeroplanes crash. Mostly they don't.
Destructuring Clojure Maps 15 Feb 2015 5:48 AM (10 years ago)
;; Destructuring Clojure's Maps ;; I can never ever remember how this works, so here is a note to self: ((fn [{a :a}] a) {:a 1}) ; 1 ;; And by let-lambda isomorphism (let [{a :a} {:a 1}] a) ; 1 ;; Why on earth is the syntax the wrong way round? Why can't {:a a} match {:a 1}? ;; Similarly ((fn [{a :a b :b}] [a b]) {:a 1 :b 2}) ; [1 2] (let [{a :a b :b} {:a 1 :b 2}] [a b]) ; ; [1 2] ;; And with the common pattern where the variables are like the keys: ((fn [{:keys [a b]}] [a b]) {:a 1 :b 2}) ; [1 2] (let [{:keys [a b]} {:a 1 :b 2}] [ a b ]) ; [1 2] ;; We can destructure recursively (although we may not be wise to if we keep forgetting how it works!) ((fn [{a :a {c :c d :d} :b}] [a c d]) {:a 1 :b {:c 2 :d 3}}) ; [1 2 3] (let [{a :a {c :c d :d} :b} {:a 1 :b {:c 2 :d 3}}] [a c d]) ; [1 2 3] ;; And we can remember the keys entire on which we have recursed, so: (let [{a :a {c :c d :d :as b} :b} {:a 1 :b {:c 2 :d 3}}] [a b c d]) ;-> [1 {:c 2, :d 3} 2 3] ;; Finally a 'real' example, a ring request map containing parameters and a session, both of ;; which have substructure (def ring-request {:params {:action "a" :key "k" :spurious "sp"} :session {:data "d" :state "s"} :irrelevant "irr"}) ;; So the parameters we're interested in look like {:params {:action :key} :session {:data :state}} ;; And we can extract all the pieces, naming each part, like so: (defn process-request [{{action :action key :key :as params } :params {data :data state :state :as session} :session :as request}] (println action) (println key) (println data) (println state) (println params) (println session) (println request)) (process-request ring-request) ;; a ;; k ;; d ;; s ;; {:key k, :action a, :spurious sp} ;; {:state s, :data d} ;; {:irrelevant irr, :params {:key k, :action a, :spurious sp}, :session {:state s, :data d}}
A Classic Puzzle 19 Oct 2014 2:08 PM (11 years ago)
;; A Classic Puzzle ;; This problem, my sources inform me, can be solved by pre-school ;; children in 5-10 minutes, by programmers - in 1 hour, and by ;; mathematicians ... well, check it yourself! :) (def input (quote ("8809" "7111" "2172" "6666" "1111" "3213" "7662" "9313" "0000" "2222" "3333" "5555" "8193" "8096" "7777" "9999" "7756" "6855" "9881" "5531"))) (map classic input) ;-> (6 0 0 4 0 0 2 1 4 0 0 0 3 5 0 4 1 3 5 0) ;; What is: (classic "2581") ;; What is classic ? ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;; Just to make it a bit easier to read (map (juxt identity classic) input) ;-> ["8809" 6] ["7111" 0] ["2172" 0] ["6666" 4] ["1111" 0] ["3213" 0] ["7662" 2] ["9313" 1] ["0000" 4] ["2222" 0] ["3333" 0] ["5555" 0] ["8193" 3] ["8096" 5] ["7777" 0] ["9999" 4] ["7756" 1] ["6855" 3] ["9881" 5] ["5531" 0]
I Wish I'd Written This 26 Jun 2014 11:39 AM (11 years ago)
Nothing specifically to do with clojure, but I figure that a fair number of readers of this blog must love algorithms and visualizations, and this:
http://bost.ocks.org/mike/algorithms/
is one of the best things I've ever read on those subjects. I really wish I'd written this! Or even was capable of writing this.
Planes In Space : Random Sampling 20 May 2014 10:19 AM (11 years ago)
;; My recursion tells me that n planes can divide space into ;; 2, 4, 8, 15, 26, and finally 42 regions. ;; But I'd like some sort of empirical confirmation of this result. ;; Forms in 3-space can be represented as ordered sets of three numbers (def a-form [1 2 3]) ;; As can vectors (def a-point [2 3 5]) ;; And we evaluate the form on the vector (defn contract [form vector] (reduce + (map * form vector))) ;; (or if you prefer, take the dot product, or contract the tensors) (contract a-form a-point) ;-> 23 ;; Any plane can be defined in terms of a 1-form and a number. (def a-plane {:form [1 2 3] :val 4}) ;; Now if we have a plane or a vector, we can evaluate the form on the ;; vector, and compare the result with the value. This tells us which ;; side of the plane the vector is on. (defn side [plane point] (- (contract (plane :form) point) (plane :val))) (side a-plane [2 3 5]) ;-> 19 (this point is on the positive side) (side a-plane [2 3 -5]) ;-> -11 (on the negative side) (side a-plane [2 3 -4/3]) ;-> 0N (in the plane itself) ;; Ok, now we need a way of taking vectors and forms at random. ;; The cauchy distribution is easy to sample from and has nice fat tails (defn cauchy[] (Math/tan (* Math/PI (- (rand) 0.5)))) (repeatedly 20 cauchy) ;-> (-0.43989542100474244 -0.6517139433588255 1.58518947555566 0.001268073580101198 3.6164981498788262 0.44928717656825584 0.3365831420089349 0.4646894211443393 0.8802485518044282 1.8146747880005754 0.1608864471756546 -0.23538854021056904 8.836583912257565 3.8174659241864703 0.5387819323291936 -0.18830386363467239 -1.0430272980416788 0.3310448308016341 -0.10735190850334911 0.3426157380908667) (defn make-point [] (repeatedly 3 cauchy)) (defn make-plane [] {:form (repeatedly 3 cauchy) :val (cauchy)}) (make-point) ;-> (33.032354006369815 -29.428219536044043 -37.796430533111334) (make-plane) ;-> {:form (-45.36910184399889 -1.6741101969009575 9.952054197916382), :val 0.9505471630252558} (def points (repeatedly #(make-point))) (def planes (repeatedly #(make-plane))) ;; And we'll need a function to tell us the sign of a number (defn sign[x] (if (< x 0) '- '+)) (map sign [ -1 -2 -3 0 -0.5 1.3]) ;-> (- - - + - +) ;; Now if we take a set of planes and a point, (defn sig [point planes] (for [p planes] (sign (side p point)))) ;; We can check which side of each plane the point is on (sig (first points) (take 3 planes)) ;-> (+ - +) ;; Every different region gives a different signature. ;; The more planes, the more signatures. (count (frequencies (take 10 (map #(sig % (take 1 planes)) points)))) ;-> 2 (count (frequencies (take 10 (map #(sig % (take 2 planes)) points)))) ;-> 4 (count (frequencies (take 10 (map #(sig % (take 3 planes)) points)))) ;-> 6 (count (frequencies (take 10 (map #(sig % (take 4 planes)) points)))) ;-> 7 (count (frequencies (take 10 (map #(sig % (take 5 planes)) points)))) ;-> 7 (count (frequencies (take 10 (map #(sig % (take 6 planes)) points)))) ;-> 7 ;; But the more planes we have, the smaller the smallest regions are ;; and thus the chance of a point falling in every one goes down. ;; The more points we take, the more likely we are to get one in every region (count (frequencies (take 100 (map #(sig % (take 1 planes)) points)))) ;-> 2 (count (frequencies (take 100 (map #(sig % (take 2 planes)) points)))) ;-> 4 (count (frequencies (take 100 (map #(sig % (take 3 planes)) points)))) ;-> 7 (count (frequencies (take 100 (map #(sig % (take 4 planes)) points)))) ;-> 11 (count (frequencies (take 100 (map #(sig % (take 5 planes)) points)))) ;-> 18 (count (frequencies (take 100 (map #(sig % (take 6 planes)) points)))) ;-> 21 (count (frequencies (take 1000 (map #(sig % (take 1 planes)) points)))) ;-> 2 (count (frequencies (take 1000 (map #(sig % (take 2 planes)) points)))) ;-> 4 (count (frequencies (take 1000 (map #(sig % (take 3 planes)) points)))) ;-> 8 (count (frequencies (take 1000 (map #(sig % (take 4 planes)) points)))) ;-> 15 (count (frequencies (take 1000 (map #(sig % (take 5 planes)) points)))) ;-> 26 (count (frequencies (take 1000 (map #(sig % (take 6 planes)) points)))) ;-> 38 (count (frequencies (take 10000 (map #(sig % (take 1 planes)) points)))) ; 2 (count (frequencies (take 10000 (map #(sig % (take 2 planes)) points)))) ; 4 (count (frequencies (take 10000 (map #(sig % (take 3 planes)) points)))) ; 8 (count (frequencies (take 10000 (map #(sig % (take 4 planes)) points)))) ; 15 (count (frequencies (take 10000 (map #(sig % (take 5 planes)) points)))) ; 26 (count (frequencies (take 10000 (map #(sig % (take 6 planes)) points)))) ; 40 (count (frequencies (take 100000 (map #(sig % (take 1 planes)) points)))) ; 2 (count (frequencies (take 100000 (map #(sig % (take 2 planes)) points)))) ; 4 (count (frequencies (take 100000 (map #(sig % (take 3 planes)) points)))) ; 8 (count (frequencies (take 100000 (map #(sig % (take 4 planes)) points)))) ; 15 (count (frequencies (take 100000 (map #(sig % (take 5 planes)) points)))) ; 26 (count (frequencies (take 100000 (map #(sig % (take 6 planes)) points)))) ; 41 (count (frequencies (take 1000000 (map #(sig % (take 1 planes)) points)))) ; 2 (count (frequencies (take 1000000 (map #(sig % (take 2 planes)) points)))) ; 4 (count (frequencies (take 1000000 (map #(sig % (take 3 planes)) points)))) ; 8 (count (frequencies (take 1000000 (map #(sig % (take 4 planes)) points)))) ; 15 (count (frequencies (take 1000000 (map #(sig % (take 5 planes)) points)))) ; 26 (count (frequencies (take 1000000 (map #(sig % (take 6 planes)) points)))) ; 42 ;; I'm painfully conscious of having stopped the experiment at the ;; exact point where I got the answer I expected. But my poor little ;; computer is not going to be up to running this for 10000000 points. ;; But this can't just be coincidence, surely?
Fizz Buzz : An Interview Question 20 May 2014 8:18 AM (11 years ago)
;; Fizz Buzz ;; My sources ;; http://blog.codinghorror.com/why-cant-programmers-program/ ;; inform me that: ;; The majority of computer science graduates can't solve this problem: ;; Write a program that prints the numbers from 1 to 100. But for ;; multiples of three print "Fizz" instead of the number and for the ;; multiples of five print "Buzz". For numbers which are multiples of ;; both three and five print "FizzBuzz". ;; And Brother Downing of this parish, who actually hires people to ;; program in Java and Clojure learns me that he does indeed use this ;; to screen job applicants, and that most of them can't do it. ;; It is hard to read a thing like that without thinking: 'hang on, is that harder than it looks?' ;; So I did it, just to check: ;; I decided to use pull it out your ass driven development, where ;; you just pull the answer out of your ass. ;; First bit, print out the numbers from 1 to 100 (range 100) ;-> (0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 ...) ;; Bugger (range 1 101) ;-> (1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 ...) ;; paranoid now (last (range 1 101)) ;-> 100 ;; Although I guess really (print (range 1 101)) is what I want ;; here. In PIOYADD, we defer this important user interface question for later. ;; Next, print 'Fizz' instead of all the multiples of three (map (= 0 #(% quot 3)) (range 1 101)) ;; ClassCastException java.lang.Boolean cannot be cast to clojure.lang.IFn clojure.core/map/fn--4207 (core.clj:2485) ;; bugger (map #(= 0 (quot % 3)) (range 1 101)) ;-> (true true false false false false false false false false false false false false false false false false false false false false false false false false false ...) ;; ok (map #(if (= 0 (quot % 3)) "Fizz" %) (range 1 101)) ;-> ("Fizz" "Fizz" 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 ...) ;; oh for fuck's sake (map #(if (= 0 (mod % 3)) "Fizz" %) (range 1 101)) ;-> (1 2 "Fizz" 4 5 "Fizz" 7 8 "Fizz" 10 11 "Fizz" 13 14 "Fizz" 16 17 "Fizz" 19 20 "Fizz" 22 23 "Fizz" 25 26 "Fizz" ...) ;; payday (map #(case (= 0 (mod % 3)) "Fizz" (= 0 (mod % 5)) "Buzz" %) (range 1 101)) ;; IllegalArgumentException No matching clause: false user/eval1234/fn--1235 (NO_SOURCE_FILE:1) ;; ok, I always screw that up (map #(cond (= 0 (mod % 3)) "Fizz" (= 0 (mod % 5)) "Buzz" %) (range 1 101)) ;; CompilerException java.lang.IllegalArgumentException: cond requires an even number of forms, compiling:(NO_SOURCE_PATH:1:7) ;; twice usually (map #(cond (= 0 (mod % 3)) "Fizz" (= 0 (mod % 5)) "Buzz" :else %) (range 1 101)) ;-> (1 2 "Fizz" 4 "Buzz" "Fizz" 7 8 "Fizz" "Buzz" 11 "Fizz" 13 14 "Fizz" 16 17 "Fizz" 19 "Buzz" "Fizz" 22 23 "Fizz" "Buzz" 26 "Fizz" ...) ;; Bwahhahhhahhh! No, Mr Bond, I expect you to die. ;; And now, for the tricky bit of the problem, we unsheathe the ;; superweapon, copy-and-paste-driven development (map #(cond (or (= 0 (mod % 3)) (= 0 (mod % 3))) "FizzBuzz" (= 0 (mod % 5)) "Buzz" :else %) (range 1 101)) ;-> (1 2 "FizzBuzz" 4 "Buzz" "FizzBuzz" 7 8 "FizzBuzz" "Buzz" 11 "FizzBuzz" 13 14 "FizzBuzz" 16 17 "FizzBuzz" 19 "Buzz" "FizzBuzz" 22 23 "FizzBuzz" "Buzz" 26 "FizzBuzz" ...) ;; hmmm (map #(cond (and (= 0 (mod % 3)) (= 0 (mod % 3))) "FizzBuzz" (= 0 (mod % 5)) "Buzz" :else %) (range 1 101)) ;-> (1 2 "FizzBuzz" 4 "Buzz" "FizzBuzz" 7 8 "FizzBuzz" "Buzz" 11 "FizzBuzz" 13 14 "FizzBuzz" 16 17 "FizzBuzz" 19 "Buzz" "FizzBuzz" 22 23 "FizzBuzz" "Buzz" 26 "FizzBuzz" ...) ;; still wrong (map #(cond (and (= 0 (mod % 3)) (= 0 (mod % 5))) "FizzBuzz" (= 0 (mod % 5)) "Buzz" :else %) (range 1 101)) ;-> (1 2 3 4 "Buzz" 6 7 8 9 "Buzz" 11 12 13 14 "FizzBuzz" 16 17 18 19 "Buzz" 21 22 23 24 "Buzz" 26 27 ...) ;; aargh, where did the fizzes go? (map #(cond (and (= 0 (mod % 3)) (= 0 (mod % 5))) "FizzBuzz" (= 0 (mod % 3)) "Fizz" (= 0 (mod % 5)) "Buzz" :else %) (range 1 101)) ;-> (1 2 "Fizz" 4 "Buzz" "Fizz" 7 8 "Fizz" "Buzz" 11 "Fizz" 13 14 "FizzBuzz" 16 17 "Fizz" 19 "Buzz" "Fizz" 22 23 "Fizz" "Buzz" 26 "Fizz" ...) ;; Wahey! That looks done. Three minutes. ;; And now, pretending you're not a filthy hacker driven development: (map #(cond (and (= 0 (mod % 3)) (= 0 (mod % 5))) "FizzBuzz" (= 0 (mod % 3)) "Fizz" (= 0 (mod % 5)) "Buzz" :else %) (range 1 101)) ;-> (1 2 "Fizz" 4 "Buzz" "Fizz" 7 8 "Fizz" "Buzz" 11 "Fizz" 13 14 "FizzBuzz" 16 17 "Fizz" 19 "Buzz" "Fizz" 22 23 "Fizz" "Buzz" 26 "Fizz" ...) (defn divides? [n m] (= 0 (mod n m))) (divides? 3 15) ;-> false ;; sigh (defn divides? [n m] (= 0 (mod m n))) (divides? 3 15) ;-> true (divides? 15 3) ;-> false ;; rah! ;; and so, behold: beauty is truth, and truth, beauty (map #(cond (divides? 15 %) "FizzBuzz" (divides? 3 %) "Fizz" (divides? 5 %) "Buzz" :else %) (range 1 101)) ;-> (1 2 "Fizz" 4 "Buzz" "Fizz" 7 8 "Fizz" "Buzz" 11 "Fizz" 13 14 "FizzBuzz" 16 17 "Fizz" 19 "Buzz" "Fizz" 22 23 "Fizz" "Buzz" 26 "Fizz" ...) ;; finally, smugness driven development: (def fizzbuzz (map #(cond (divides? 15 %) "FizzBuzz" (divides? 3 %) "Fizz" (divides? 5 %) "Buzz" :else %) (map inc (range)))) ;; There are those who would call this 'premature abstraction', but they deserve not the names of men. (print (take 100 fizzbuzz)) ;; (1 2 Fizz 4 Buzz Fizz 7 8 Fizz Buzz 11 Fizz 13 14 FizzBuzz 16 17 Fizz 19 Buzz Fizz 22 23 Fizz Buzz 26 Fizz ...) ;; And I suppose a regression test would be nice, if I'm trying to ;; give some sort of professional impression: (= (take 27 fizzbuzz) (list 1 2 "Fizz" 4 "Buzz" "Fizz" 7 8 "Fizz" "Buzz" 11 "Fizz" 13 14 "FizzBuzz" 16 17 "Fizz" 19 "Buzz" "Fizz" 22 23 "Fizz" "Buzz" 26 "Fizz")) ;; And some paranoid checks, if I'm going to put this travesty on my blog: (count (filter #(= "Fizz" %) (take 1000 fizzbuzz))) ; -> 267 (count (filter #(= "FizzBuzz" %) (take 1000 fizzbuzz))) ;-> 66 (count (filter #(= "Buzz" %) (take 1000 fizzbuzz))) ;-> 134 (* (+ 134 66) 5) ;-> 1000 (* (+ 267 66) 3) ;-> 999 ;; bah, that's close enough for government work. I declare myself ;; done. Three minutes of flail and two minutes of tidying up and ;; checking it works. ;; So my question to the wider community is: Does my three minutes of ;; flailing trying to remember the semantics of my favourite language ;; (which I can perfectly imagine looking dreadful at an interview) ;; count as a fail or a pass? ;; In a previously unknown assembly language, but given a library to ;; print numbers on the screen, I can imagine taking half an hour to ;; get this working. Without the library, it's a research project. ;; And obviously, if I tried to do it in Haskell, I'd have to spend ;; three weeks remembering what a monad was in order to print the ;; damned thing out, but at least the type system would magically ;; guarantee the correctness of the final program. ;; In other words, is fizzbuzz really actually quite hard, or is ;; everyone out there a complete idiot?
Planes in Space : Checking by Hand 12 May 2014 2:43 PM (11 years ago)
;; Ok, so I reckon: (defn regions [n m] (cond (= n 1) (list m (inc m)) (= m 0) (concat (repeat n 0) '(1)) :else (map + (regions n (dec m)) (concat '(0) (regions (dec n) (dec m))) (concat (regions (dec n) (dec m)) '(0))))) ;; In fact, I reckon that I can prove it. ;; It's quite easy to prove something that isn't true. Usually when ;; you run across a counterexample, that shows you where the ;; unsuspected false step in your reasoning was. ;; So I'd like to verify the formula on lots of examples. ;; But how? ;; These I can count in my head. (regions 3 0) ;-> (0 0 0 1) ; just space, no planes (regions 3 1) ;-> (0 0 1 2) ; a plane cuts space in half (regions 3 2) ;-> (0 1 4 4) ; two planes intersect in one line, cutting space into four (regions 3 3) ;-> (1 6 12 8) ; 1 point where three planes meet, ; six coordinate half-axes, ; three coordinate planes divided into four quadrants each, ; and eight octants ;; I am sort of confident that four planes make fifteen regions and intersect in four points. (regions 3 4) ;-> (4 18 28 15) ;; But every attempt to count the 18 lines and 28 regions I make ends up relying on ;; the sort of arguments I made to make the recursion in the first place. ;; And at this point my intuition breaks. (regions 3 5) ;-> (10 40 55 26) ;; I mean, five planes, any three intersect in a point, ;; 10 ways to choose 3 planes from five, so 10 points, ;; but after that I'm dead. ;; And this? Six choose 3 is 20, I can see that.... (regions 3 6) ;-> (20 75 96 42) ;; And I defy anyone to even picture (regions 5 8) ;-> (56 350 896 1176 792 219) ;; 8 choose 5 is (/ (* 8 7 6) (* 1 2 3)) = 56, which is fair enough. ;; 8 choose 4 is (/ (* 8 7 6 5) (* 1 2 3 4)) is 70 ;; If we take any 4 hyperplanes from our 8, they'll define a line. ;; The four remaining hyperplanes then divide each line like: (regions 1 4) ;-> (4 5) ;; So if each of those lines is sliced into 5 pieces then that's our 350. ;; But I'm just using the same recursive argument again. ;; So I don't even know if that's evidence or not. ;; One nice thing about it, the formula has an alternating sum property, ;; like the Euler index. (defn signature [lst] (reduce + (map * (apply concat (repeat '(+1 -1))) (reverse lst)))) (signature (regions 5 8)) ;-> 1 (def regions (memoize regions)) (regions 7 23) ;-> (245157 1817046 5787628 10271800 10973116 7057688 2531288 390656) (signature (regions 7 23)) ;-> 1 (regions 23 20) ;-> (0 0 0 1 40 760 9120 77520 496128 2480640 9922560 32248320 85995520 189190144 343982080 515973120 635043840 635043840 508035072 317521920 149422080 49807360 10485760 1048576) (signature (regions 23 20)) ;-> 1 ;; But annoyingly, you can just read that property straight from the recursion!
Planes in Spaaace! 30 Apr 2014 5:38 AM (11 years ago)
;; Into how many regions can six planes divide space? ;; Too hard! ;; So make it harder: ;; Into how many regions can m hyperplanes divide n dimensional space? ;; Now look at the easiest case. ;; Into how many lines can m points divide a line? ;; We start off with one line and no points ;; n = 1 ;; m points lines ;; 0 0 1 ;; Every time we add a point, it splits a line ;; n = 1 ;; m points lines ;; 0 0 1 ;; 1 1 2 ;; 1 1 2 (defn regions [n m] (cond (= n 1) (list m (inc m)) :else 'chsaispas)) (regions 1 10) ;-> (10 11) ;; Adding ten points turns a line into 11 lines and 10 points. ;; Ok, what about lines dividing a plane? ;; We start off with one area, no lines and no points. ;; n = 2 ;; m points lines areas ;; 0 0 0 1 ;; When we add a line, it splits the area into two areas, so we have ;; no points, one line and two areas ;; n = 2 ;; m points lines areas ;; 0 0 0 1 ;; 1 0 1 2 ;; When we add a second line, unless we've accidentally put it ;; parallel to our first line, in which case we aren't doing as well ;; as we could do, it will cross the first line. ;; So our new line will be actually be one point and two lines, ;; and the one point will divide the first line in two, ;; and the two lines will cut the two areas into four. ;; 0 1 2 ;; State with one line ;; 1 2 ;; Added one point and two lines ;; 1 2 ;; Which have split one line and two areas ;; 1 4 4 ;; So two lines divide a plane into one point, four lines and four areas ;; n = 2 ;; m points lines areas ;; 0 0 0 1 ;; 1 0 1 2 ;; 2 1 4 4 ;; When we add a third line, it will cross both previous lines, and so it will be ;; a line divided by two points (regions 1 2) ;-> (2 3) (map + '(1 4 4) (concat '(0) (regions 1 2)) (concat (regions 1 2) '(0))) ;-> (3 9 7) ;; If you draw the figure, you'll see that it indeed has a triangle with three vertices, ;; which split the three lines into 9, and there are seven distinct regions. ;; So, taking a blind leap in the dark... (defn regions [n m] (cond (= n 1) (list m (inc m)) (= m 0) (concat (repeat n 0) '(1)) :else (map + (regions n (dec m)) (concat '(0) (regions (dec n) (dec m))) (concat (regions (dec n) (dec m)) '(0))))) (regions 1 0) ;-> (0 1) (regions 1 1) ;-> (1 2) (regions 1 2) ;-> (2 3) (regions 1 3) ;-> (3 4) (regions 2 0) ;-> (0 0 1) (regions 2 1) ;-> (0 1 2) (regions 2 2) ;-> (1 4 4) (regions 2 3) ;-> (3 9 7) (regions 2 4) ;-> (6 16 11) (regions 2 5) ;-> (10 25 16) (regions 3 1) ;-> (0 0 1 2) (regions 3 2) ;-> (0 1 4 4) (regions 3 3) ;-> (1 6 12 8) (regions 3 4) ;-> (4 18 28 15) (regions 3 5) ;-> (10 40 55 26) (regions 3 6) ;-> (20 75 96 42) ;; Into how many regions can six planes divide space? (last (regions 3 6)) ;-> 42
Into How Many Regions Can Six Planes Divide Space? 30 Apr 2014 4:21 AM (11 years ago)
I recently misread an easy recreational puzzle as 'Into how many regions can six planes divide space?'.
It
took me about half an hour to get an answer. (Which was the correct
answer to the question, but not the answer to the real puzzle). But it
turned out to be great fun to think about.
I'm pretty
sure that my answer's correct (and wikipedia agrees), but although the
combination of mathematical proof and worldwide consensus should probably
be enough, I'm never really convinced by a mathematical
idea until I've seen it confirmed by lots of examples.
So
I've got programs planned, and if they turn out well, then
I'll post them here. But they won't be any fun to read unless you've
tried to work it out yourself.
If it's not clear, the idea is that you've got a big block of sponge cake, and a very large knife, and you want to cut it into as many pieces as possible with six cuts.
So if the problem said 'one' rather than 'six', the answer would be two, and if it said 'two', then the answer would be 'four'.
1,2,4,8,..... how does this sequence continue?
Finite Automata 9 Jan 2014 1:51 PM (12 years ago)
I did some pictures of automata to go with this post, but Google have managed to bugger up 'Insert Image' in Blogger, which used to be easy.
I wonder if their monkeys are even interested in whether their filthy javascript crap actually works before they inflict it on people.
God I hate them. They've gone from 'Don't be evil / Awesome' to 'We own you now / But we can't program any more' in a couple of years.
I'd really like to move this blog somewhere less incompetent. Anyone got any suggestions?
You'll just have to imagine what the pictures look like. Think bubbles and arrows.
;; Finite Automata ;; I just did Jeff Ullmann's Stanford Course 'Automata' through Coursera. It was fascinating. ;; A finite automaton is a mathematical model representing a simple ;; computer. But it's very close to being a computer. In fact you can ;; code them up in Verilog and make them out of silicon. In chip ;; design they're known as finite state machines. ;; They're strictly less powerful than real computers and programs, ;; but they can still do lots of stuff. On the other hand, we can ;; determine what it is that they do much more easily than we can with ;; computers and programs. ;; Here's an example of an automaton ;; Start at A ;; A -0-> A ;; A -1-> B ;; B -1-> B ;; B -0-> A ;; B is an accepting state ;; INSERT IMAGE automaton1.png (def automatonI {:start :A :accept #{:B} :transition { 1 {:A :B :B :B} 0 {:A :A :B :A}}}) ;; How should we work out whether this automaton accepts the string 101101011 ? ;; It starts in state :A (automatonI :start) ;-> :A ;; The first character of the string is a 1, and so it transitions to B (((automatonI :transition) 1) (automatonI :start)) ;-> :B ;; The second character is 0, so it transitions back to :A (((automatonI :transition) 0) (((automatonI :transition) 1) (automatonI :start))) ;-> :A ;; And so on (reduce (fn[state input] (((automatonI :transition) input) state)) (automatonI :start) (list 1 0 1 1 0 1 0 1 1)) ;-> :B ;; The final state after all the input is consumed is :B, which is an accepting state (defn final-state [automaton string] (reduce (fn[state input] (((automaton :transition) input) state)) (automaton :start) string)) (final-state automatonI (list 1 0 1 1 0 1 0 1 1)) ;-> :B (final-state automatonI (list 1 0 1 1 0 1 0 1 0)) ;-> :A ;; And so the string 101101011 is accepted by the automaton. (defn accepts [automaton string] (not (nil? ((automaton :accept) (final-state automaton string))))) (accepts automatonI (list 1 0 1 1 0 1 0 1 1)) ;-> true (accepts automatonI (list 1 0 1 1 0 1 0 1 0)) ;-> false ;; We might ask what other strings are accepted ;; First let's generate all possible strings of zeros and ones (defn extend [ss] (for [a ss b '(0 1)] (cons b a))) (extend '(())) ;-> ((0) (1)) (extend (extend '(()))) ;-> ((0 0) (1 0) (0 1) (1 1)) ;; All these strings together are rather charmingly known as the free monoid on #{0,1} ;; But enough of that! We know what strings are! (def strings01 (apply concat (iterate extend '(())))) strings01 ;-> (() (0) (1) (0 0) (1 0) (0 1) (1 1) (0 0 0) (1 0 0) (0 1 0) (1 1 0) (0 0 1) (1 0 1) (0 1 1) (1 1 1) (0 0 0 0) (1 0 0 0) (0 1 0 0) (1 1 0 0) (0 0 1 0) (1 0 1 0) (0 1 1 0) (1 1 1 0) (0 0 0 1) (1 0 0 1) (0 1 0 1) (1 1 0 1) ...) ;; As you may have guessed, this automaton accepts strings that end in 1 (filter (partial accepts automatonI) strings01) ;-> ((1) (0 1) (1 1) (0 0 1) (1 0 1) (0 1 1) (1 1 1) (0 0 0 1) (1 0 0 1) (0 1 0 1) (1 1 0 1) (0 0 1 1) (1 0 1 1) (0 1 1 1) (1 1 1 1) (0 0 0 0 1) (1 0 0 0 1) (0 1 0 0 1) (1 1 0 0 1) (0 0 1 0 1) (1 0 1 0 1) (0 1 1 0 1) (1 1 1 0 1) (0 0 0 1 1) (1 0 0 1 1) (0 1 0 1 1) (1 1 0 1 1) ...) ;; Proof by trying a finite number of cases: (map last (filter (partial accepts automatonI) strings01)) ;-> (1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ...) (map last (filter (comp not (partial accepts automatonI)) strings01)) ;-> (nil 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ...) ;; Here's a (slightly) more interesting variant: ;; INSERT AUTOMATONII.PNG (def automatonII {:start :A :accept #{:B} :transition { 1 {:A :B :B :A} 0 {:A :A :B :B}}}) ;; Can you see what it is doing? (filter (partial accepts automatonII) strings01) ;-> ((1) (1 0) (0 1) (1 0 0) (0 1 0) (0 0 1) (1 1 1) (1 0 0 0) (0 1 0 0) (0 0 1 0) (1 1 1 0) (0 0 0 1) (1 1 0 1) (1 0 1 1) (0 1 1 1) (1 0 0 0 0) (0 1 0 0 0) (0 0 1 0 0) (1 1 1 0 0) (0 0 0 1 0) (1 1 0 1 0) (1 0 1 1 0) (0 1 1 1 0) (0 0 0 0 1) (1 1 0 0 1) (1 0 1 0 1) (0 1 1 0 1) ...) ;; And finally: (def automatonIII {:start :A :accept #{:A} :transition { 1 {:A :B :B :A :C :C} 0 {:A :A :B :C :C :B}}}) ;; INSERT AUTOMATONIII.PNG (filter (partial accepts automatonIII) strings01) ;-> (() (0) (0 0) (1 1) (0 0 0) (1 1 0) (0 1 1) (0 0 0 0) (1 1 0 0) (0 1 1 0) (1 0 0 1) (0 0 1 1) (1 1 1 1) (0 0 0 0 0) (1 1 0 0 0) (0 1 1 0 0) (1 0 0 1 0) (0 0 1 1 0) (1 1 1 1 0) (0 1 0 0 1) (1 0 1 0 1) (0 0 0 1 1) (1 1 0 1 1) (0 1 1 1 1) (0 0 0 0 0 0) (1 1 0 0 0 0) (0 1 1 0 0 0) ...) ;; Can you see what this one is doing? ;; Here's a clue (defn to-integer [lst] (cond (empty? lst) 0 (= (first lst) 1) (+ 1 (* 2 (to-integer (rest lst)))) :else (* 2 (to-integer (rest lst))))) (map to-integer strings01) (map to-integer (filter (partial accepts automatonIII) strings01)) ;-> (0 0 0 3 0 3 6 0 3 6 9 12 13 15 0 3 6 9 12 13 15 18 24 26 27 30 0 ...) (for [[k v] (group-by (partial accepts automatonIII) (take 100 strings01))] [k (sort (distinct (map to-integer v)))]) ;;-> ([true (0 3 6 9 12 15 18 21 24 27 30 33 36)] ;; [false (1 2 4 5 7 8 10 11 13 14 16 17 19 20 22 23 25 26 28 29 31 32 34 35)]) ;; Can you get it to work the right way round? ;; Can you generalize it?